Тригонометрия – одна из самых сложных разделов математики, который сталкивает многих студентов с трудностями. Если ты путаешь синусы, косинусы и тангенсы, не можешь решить задачу на нахождение угла или просто заплутал в море тригонометрических формул, не отчаивайся! Мы поможем тебе разобраться в этой науке и освоить все ее тайны!
Первое, что нужно понять, – это основные понятия тригонометрии. Синус, косинус и тангенс – это отношения длин сторон прямоугольного треугольника, а углы и радианы – единицы измерения. Изучение этих понятий поможет тебе понять сути тригонометрии и правильно применять ее в задачах.
Второе, что необходимо сделать, чтобы научиться понимать тригонометрию, – это много практиковаться. Решай задачи, выполняй упражнения, анализируй примеры. Только практика поможет тебе закрепить теоретические знания и улучшить свои навыки. Не отказывайся от дополнительных занятий, в которых ты сможешь практиковаться под руководством опытных преподавателей.
Понятие тригонометрии и ее роль в математике

Основной объект изучения в тригонометрии – это треугольник. Тригонометрические функции (синус, косинус, тангенс, котангенс, секанс, косеканс) определяются отношениями длин сторон треугольника. Они позволяют связать углы и стороны треугольника и использовать их для решения разнообразных задач и проблем.
Тригонометрия находит широкое применение в решении геометрических, физических и инженерных задач. К примеру, с помощью тригонометрии можно рассчитать расстояние между двумя объектами, определить высоту недоступных объектов, решить задачи на геодезии и навигации, моделировать колебания, определять координаты точек на плоскости и многое другое.
Тригонометрия также является основой для изучения более сложных математических концепций, таких как теория функций, комплексный анализ и теория вероятности. Наличие знаний тригонометрии позволяет углубить понимание и применение этих высших математических теорий и методов.
В целом, понимание тригонометрии является важным элементом математической подготовки и способствует осознанному аналитическому мышлению. Оно не только помогает решать задачи в науке и технике, но и развивает логическое мышление и абстрактное мышление, что является ценным во многих сферах жизни.
Основные тригонометрические функции и их геометрический смысл
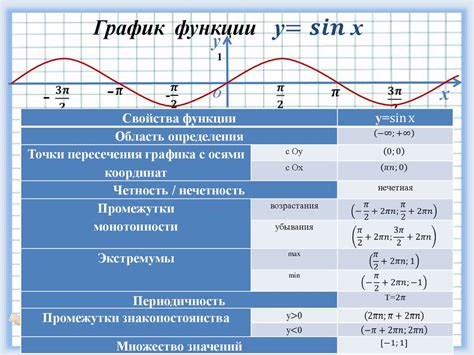
Одной из основных тригонометрических функций является синус (sin). Синус угла равен отношению противоположной стороны к гипотенузе в прямоугольном треугольнике. Таким образом, sin A = a / c, где A - угол, a - противоположная сторона, c - гипотенуза.
Косинус (cos) угла равен отношению прилежащей стороны к гипотенузе. То есть, cos A = b / c, где b - прилежащая сторона.
Тангенс (tg) угла равен отношению противоположной стороны к прилежащей. То есть, tg A = a / b.
Котангенс (ctg) является обратной функцией к тангенсу и равен отношению прилежащей стороны к противоположной. То есть, ctg A = b / a.
Секанс (sec) и косеканс (csc) - это обратные функции к косинусу и синусу соответственно. Секанс угла равен отношению гипотенузы к прилежащей стороне, а косеканс - к гипотенузе и противоположной стороне.
Знание основных тригонометрических функций и их геометрического смысла позволяет решать различные задачи, связанные с углами и сторонами треугольников, такие как нахождение неизвестных сторон или углов, определение равенства треугольников и многое другое.
Применение тригонометрии в решении задач различных областей
В физике тригонометрия широко используется для измерения и моделирования различных физических явлений. Например, при изучении движения тела в пространстве важно знать углы и расстояния между объектами. Тригонометрические функции, такие как синус и косинус, позволяют решать эти задачи и предсказывать поведение системы.
В инженерии тригонометрия используется для решения задач, связанных с построением и проектированием. Например, при строительстве мостов или зданий важно знать углы и длины сторон для правильного выравнивания и размещения элементов конструкции.
Астрономия - еще одна область, где тригонометрия играет ключевую роль. С помощью тригонометрии можно измерять расстояния до звезд и планет, а также определять их координаты на небесной сфере. Это помогает астрономам составлять карты ночного неба и предсказывать события, такие как затмения и прохождения планет.
Картография - наука, которая занимается созданием и анализом карт. Тригонометрические методы используются для измерения расстояний и углов на земной поверхности, а также для построения точных картографических проекций. Это позволяет создавать детализированные карты, которые используются в навигации, геодезии и планировании городского развития.



