Углы и стороны треугольника взаимосвязаны между собой специальными математическими соотношениями. Если известен один из углов треугольника, можно использовать тригонометрическую функцию для расчета стороны напротив этого угла.
Для треугольника, у которого один из углов равен 30 градусам, используется специальное соотношение, известное как "отношение сторон 30-60-90 градусного треугольника". В таком треугольнике сторона напротив угла в 30 градусов всегда равна половине длины гипотенузы.
Давайте обозначим сторону напротив угла в 30 градусов как "a" и гипотенузу как "c". Тогда, согласно формуле, a = (c * sin(30°))/2. Также, используя другую тригонометрическую функцию, в этом выражении можно заменить sin(30°) на cos(60°), что даст a = (c * cos(60°))/2.
Теперь вы можете использовать эту формулу и известное значение гипотенузы, чтобы вычислить сторону треугольника напротив угла в 30 градусов. Помните, что значение гипотенузы должно быть известно, чтобы выполнить расчет.
Чему равна сторона напротив 30 градусного угла в треугольнике - формула и расчет

Чтобы найти сторону напротив 30 градусного угла в треугольнике, необходимо использовать тригонометрическую формулу. Данная формула называется теоремой синусов, и она позволяет найти отношение длин сторон треугольника к синусам соответствующих углов.
Формула теоремы синусов имеет вид: с/а = sin(С)/sin(А), где:
- с - сторона напротив угла С
- а - сторона напротив угла А
- С - угол, напротив которого находится сторона с
- А - угол, напротив которого находится сторона а
Таким образом, чтобы найти сторону напротив 30 градусного угла, необходимо знать длину другой стороны и значение угла, напротив которого она находится. Подставив известные значения в формулу и решив ее, можно найти значением стороны.
Например, если известна длина стороны а и угол А, а требуется найти длину стороны с, можно воспользоваться формулой теоремы синусов и рассчитать значение.
| Известно | Формула | Расчет |
|---|---|---|
| а | с/а = sin(С)/sin(А) | с = а * sin(С) / sin(А) |
Рассчитав значение с помощью данной формулы, можно определить длину стороны напротив 30 градусного угла в треугольнике.
Геометрия: треугольник и его углы
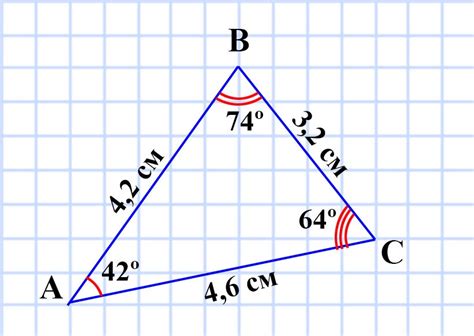
В треугольнике существуют различные способы определения значений углов. Один из них - использование формулы для расчета стороны треугольника, если известен угол. Для этого можно использовать тригонометрические соотношения, такие как синус, косинус и тангенс.
Допустим, в треугольнике известен угол, например, 30 градусов. Чтобы найти значение стороны, находящейся напротив этого угла, можно воспользоваться формулой:
сторона = синус(угол) * гипотенуза
В данной формуле "гипотенуза" обозначает самую длинную сторону треугольника, а "синус(угол)" означает значение синуса угла (в данном случае синус угла 30 градусов).
На основании данной формулы можно легко вычислить значение стороны, напротив угла 30 градусов, в данном треугольнике.
Тригонометрия: определение и основные понятия

Основные понятия тригонометрии включают углы, стороны треугольника и тригонометрические функции. Углы могут быть измерены в градусах или радианах. В треугольнике существуют три стороны: гипотенуза, напротив которой находится прямой угол, и две катеты. Катеты могут быть прилегающими и противоположными, в зависимости от расположения относительно угла.
Самыми распространенными тригонометрическими функциями являются синус (sin), косинус (cos) и тангенс (tg). Они определяются отношениями между сторонами треугольника. Например, sin угла равен отношению противоположной стороны к гипотенузе.
| Тригонометрическая функция | Определение |
|---|---|
| Синус (sin) | Отношение противоположной стороны к гипотенузе |
| Косинус (cos) | Отношение прилегающей стороны к гипотенузе |
| Тангенс (tg) | Отношение противоположной стороны к прилегающей стороне |
Тригонометрия имеет много приложений в различных областях науки и техники. Она используется для решения проблем навигации, построения карт, анализа колебаний и волн, а также для моделирования физических процессов.
Итак, тригонометрия - это инструмент, который позволяет изучать и анализировать углы и стороны треугольников, а также применять полученные знания в различных областях науки и техники.
Синус угла: формула и свойства
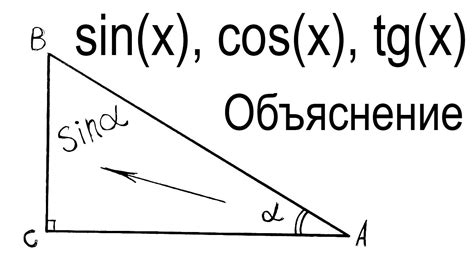
sin(a) = противоположный катет / гипотенуза
Свойства синуса угла:
- Значение синуса угла всегда находится в диапазоне от -1 до 1
- Если угол равен 0 градусов, то синус угла равен 0
- Если угол равен 90 градусов, то синус угла равен 1
- Если угол равен 180 градусов, то синус угла равен 0
- Если угол равен 270 градусов, то синус угла равен -1
- Если угол равен 360 градусов, то синус угла равен 0
- Значение синуса угла может быть отрицательным, если угол находится во 2-й или 3-й четверти
- Значение синуса угла может быть положительным, если угол находится в 1-й или 4-й четверти
Синус угла является важным понятием при решении задач, связанных с треугольниками и колебаниями.
Теорема синусов: описание и применение

Теорема синусов утверждает, что отношение длины стороны треугольника к синусу противолежащего ей угла для всех сторон треугольника будет одинаково:
a/sin A = b/sin B = c/sin C
Здесь a, b и c – длины сторон треугольника, A, B и C – соответствующие им углы.
Теорему синусов можно использовать для решения различных задач с треугольниками. Например, зная две стороны треугольника и угол между ними, можно найти длину третьей стороны, применяя формулу теоремы синусов. Аналогично, если известны три стороны треугольника, можно найти значения всех его углов, используя соответствующие формулы.
Теорема синусов также может применяться для вычисления площади треугольника. Формула для этого выглядит следующим образом:
S = (1/2) * a * b * sin C
Здесь S – площадь треугольника, a и b – длины двух сторон треугольника, C – угол между этими сторонами.
Таким образом, теорема синусов является полезным инструментом в геометрии, который позволяет решать различные задачи с треугольниками и вычислять их геометрические параметры.
Формула нахождения стороны треугольника по синусу угла
Для нахождения стороны треугольника, напротив заданного угла, по синусу этого угла можно использовать следующую формулу:
сторона = (длина другой стороны * синус угла) / синус другого угла
Например, если нам известны длина стороны треугольника, напротив которой находится угол 30 градусов, и длина другой стороны, а также мера угла противолежащего этой стороне:
- Длина стороны треугольника, напротив угла 30 градусов: a
- Длина другой стороны треугольника: b
- Угол противолежащий стороне b: A
Тогда мы можем использовать формулу:
a = (b * sin(30)) / sin(A)
Значения синусов углов можно найти в таблице синусов. Подставив эти значения в формулу, мы получим значение стороны треугольника, напротив угла 30 градусов.
Расчет стороны треугольника с углом 30 градусов
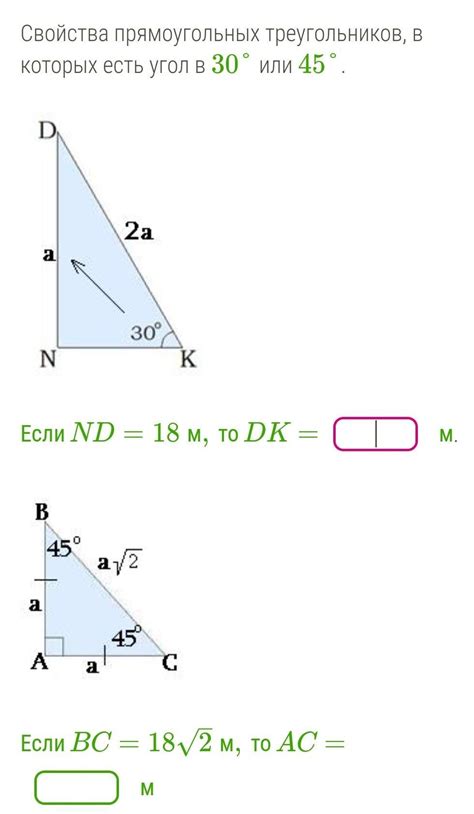
Если в треугольнике имеется угол в 30 градусов, то возможно использование формулы синуса для расчета стороны напротив данного угла.
Формула для расчета стороны принимает вид:
a = c * sin(30°)
Где a - искомая сторона треугольника, c - длина гипотенузы, а 30° - известный угол.
Для точного расчета стороны требуется знание длины гипотенузы, аргумента синуса угла 30° и таблицы значений синуса.
Например, если гипотенуза равна 10 единицам, то формула примет вид:
a = 10 * sin(30°)
Теперь необходимо найти значение синуса угла 30°. В таблице находим, что sin(30°) равен 0.5.
Тогда окончательная формула приобретает вид:
a = 10 * 0.5 = 5
Таким образом, сторона треугольника напротив угла в 30 градусов равна 5 единицам.
Примеры вопросов и решений
Вот несколько примеров вопросов и решений, связанных с нахождением стороны напротив угла в треугольнике с углом 30 градусов:
Пример 1:
Дан треугольник ABC, в котором угол B равен 30 градусов, сторона AC равна 5 сантиметров, а сторона BC равна 10 сантиметров. Найдите сторону AB.
Решение:
Для решения этой задачи можно воспользоваться теоремой синусов. Согласно этой теореме, отношение длины стороны к синусу противолежащего угла постоянно в треугольниках. Таким образом, мы можем записать следующее равенство:
(AB / sin(30 градусов)) = (AC / sin(угол CAB))
Зная значения сторон и угла, мы можем выразить длину стороны AB:
AB = (5 сантиметров * sin(30 градусов)) / sin(угол CAB)
Пользуясь тригонометрическими таблицами или калькулятором, можно вычислить значение синуса 30 градусов и угла CAB. Далее, подставив значения в формулу, мы получим ответ.
Пример 2:
Треугольник A'BC' является подобным треугольнику ABC, причем угол B равен 30 градусов, сторона AC равна 8 сантиметров, а сторона BC равна 12 сантиметров. Найдите длину стороны A'B'.
Решение:
Поскольку треугольник A'BC' подобен треугольнику ABC, отношения длин соответствующих сторон должны быть равны. Используя эту информацию и теорему синусов, мы можем записать следующее равенство:
(A'B' / AB) = (C'B' / BC)
AB = (8 сантиметров * sin(30 градусов)) / sin(угол CAB)
Пользуясь тригонометрическими таблицами или калькулятором, можно вычислить значение синуса 30 градусов и угла CAB. Далее, подставив значения в формулу, мы можем найти длину стороны A'B'.



