Окружность, вписанная в угол, является особым геометрическим объектом, который играет важную роль в различных областях науки и техники. Дуга окружности, вписанной в угол, определяется как часть окружности, которая находится внутри этого угла. Но как можно вычислить длину такой дуги и чему она равна?
Для вычисления длины дуги окружности вписанной в угол необходимо знать радиус этой окружности и величину угла, в который эта окружность вписана. Формула для вычисления длины дуги окружности называется дуговой формулой и выглядит следующим образом:
Длина дуги = (радиус окружности) x (величина угла в радианах)
Таким образом, чтобы найти длину дуги окружности вписанной в угол, необходимо умножить радиус окружности на величину угла в радианах. Радианы являются удобной мерой для измерения углов, так как они связаны с радиусом окружности.
Окружность вписанная в угол
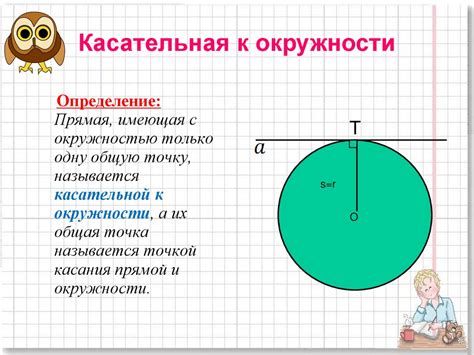
Чтобы найти длину дуги окружности, нужно знать ее радиус и угол, на который она охватывает.
Давайте рассмотрим пример. Пусть у нас есть угол с вершиной O и двумя сторонами OA и OB. Допустим, окружность вписанная в этот угол имеет радиус r и центр в точке C.
 |  |
Так как окружность касается обеих сторон угла, то от центра окружности C к точке касания с OA, обозначим ее точкой E, проведем перпендикуляр. Аналогично проведем перпендикуляр от C до точки касания с OB, обозначим ее точкой F.
Так как у равнобедренного треугольника OCЕ прямоугольный угол, то OE является радиусом окружности и его длина r. Аналогично CF также радиус и его длина также r.
Так как центр окружности находится на биссектрисе угла, то OD будет являться bis(OAB) и угол BAD будет равным половине угла B.
Теперь мы можем найти дугу AD, которую охватывает окружность. Для этого нужно вычислить угол AOD. Для простоты представим радиус r = 1. Тогда OD = tan(BAD) = tan(ODA) = tan(B/2).
Таким образом, длина дуги AD равна углу AOD, умноженному на радиус r. Формула для вычисления дуги AD будет следующей:
Дуга AD = AOD * r
Таким образом, мы можем легко найти длину дуги окружности вписанной в угол, зная радиус и угол, на который эта дуга охватывает.
Геометрическое свойство окружности
Одним из интересных свойств окружности является связь между дугой окружности и углом, образованным этой дугой. Когда окружность вписана внутрь угла, дуга окружности, заключенная в этом угле, равна половине угла в радианах, умноженной на радиус окружности.
Это свойство может быть выражено математической формулой:
Дуга окружности = (Угол / 2) * Радиус
Например, если у нас есть окружность радиусом 5 и угол между касательными к этой окружности равен 60 градусам, то дуга окружности вписанная в этот угол будет равна:
Дуга окружности = (60 / 2) * 5 = 30 * 5 = 150
Таким образом, дуга окружности, вписанная в угол, вычисляется путем деления угла на два и умножения результата на радиус окружности.
Определение дуги окружности
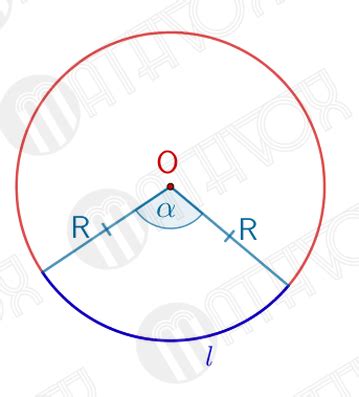
Угол, определяющий дугу окружности, называется центральным углом. Он измеряется в градусах, радианах или градах и определяет, какую часть окружности занимает данная дуга.
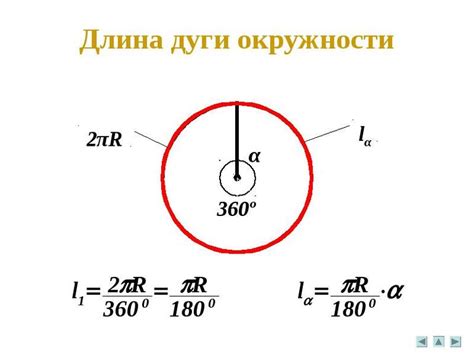
Длина дуги окружности зависит от радиуса окружности и центрального угла. Формула для вычисления длины дуги окружности имеет вид:
L = 2πr * (θ / 360)
где L - длина дуги окружности, π - математическая константа, приближенно равная 3,14159, r - радиус окружности, θ - центральный угол в градусах.
Математическая формула для расчета длины дуги
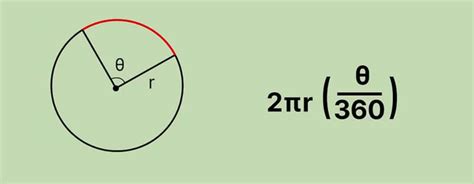
Существует математическая формула, которая позволяет нам вычислить длину дуги:
| Формула | Описание |
|---|---|
| l = r * α | где l - длина дуги, r - радиус окружности, α - угол в радианах |
Данную формулу можно применить, когда известен радиус окружности и угол, под которым лежит дуга. Угол α должен быть выражен в радианах, так как радиан - это оптимальная единица измерения в геометрии и тригонометрии.
Длина дуги зависит от радиуса окружности и угла под которым лежит дуга. Чем больше радиус или угол, тем длиннее будет дуга. Эта формула особенно полезна при решении задач, связанных с геометрией и тригонометрией, и может быть использована для расчета длины дуги окружности вписанной в угол.
Примеры расчета длины дуги окружности
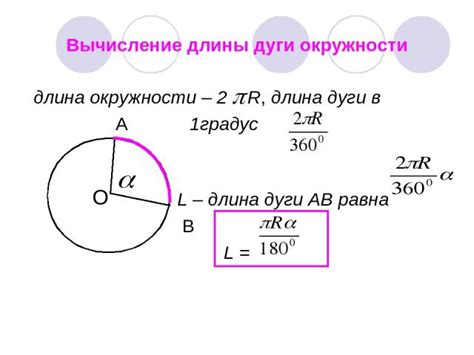
Длина дуги окружности может быть рассчитана с использованием формулы:
L = 2πr∙(α/360)
где L - длина дуги, r - радиус окружности, α - центральный угол в градусах.
Рассмотрим несколько примеров:
Пример 1:
Дана окружность с радиусом 5 см и центральным углом α = 60°.
L = 2π∙5∙(60/360) = 2π∙5∙(1/6) = π/3 ≈ 1.04 см
Пример 2:
Дана окружность с радиусом 8 м и центральным углом α = 45°.
L = 2π∙8∙(45/360) = 2π∙8∙(1/8) = π м ≈ 3.14 м
Пример 3:
Дана окружность с радиусом 10 дм и центральным углом α = 120°.
L = 2π∙10∙(120/360) = 2π∙10∙(1/3) = (20/3)π дм ≈ 20.94 дм
Таким образом, используя указанную формулу, можно рассчитать длину дуги окружности при заданном радиусе и центральном угле.
Применение дуги окружности в задачах
Дуга окружности, вписанной в угол, находит свое применение во множестве задач различных областей.
Одним из примеров применения дуги окружности в задачах является геометрия. Когда нам известен радиус окружности и угол, на котором расположена дуга, мы можем вычислить длину этой дуги, используя соответствующую формулу. Это позволяет решать задачи, связанные с определением площадей и объемов фигур, а также нахождением расстояний и времени, связанных с движением по окружности.
- Третий пример – использование дуги окружности в задачах, связанных с строительством и архитектурой. Дуги окружности часто используются для создания арок и окон в зданиях. Они могут придать зданию элегантность и красоту, а также обеспечить определенный функционал, например, обеспечивая поддержку крыши или служа как декоративный элемент.
- В четвертом примере мы можем рассмотреть применение дуги окружности в программировании и компьютерной графике. Дуги окружности часто используются для создания анимаций, визуализации данных и построения графических интерфейсов. Они могут быть использованы для отображения прогресса выполнения задачи, представления диаграмм и графиков, а также для создания интерактивных элементов пользовательского интерфейса.



