Прямоугольный треугольник - это геометрическая фигура, у которой один из углов равен 90 градусам. В таком треугольнике есть ряд свойств, которые позволяют вычислить различные его параметры. Одним из таких параметров является медиана.
Медиана треугольника – это прямая, соединяющая вершину треугольника с серединой противоположной стороны. В прямоугольном треугольнике с медианой все несколько сложнее, поскольку она там имеет специфическую форму и определенную длину, которую мы можем вычислить с помощью простой формулы.
Для вычисления длины медианы в прямоугольном треугольнике необходимо знать длины его сторон. Пусть a и b – это длины катетов, а c – это длина гипотенузы. В этом случае медиана треугольника равна половине длины гипотенузы ∣∣.
Расчёт длины медианы в прямоугольном треугольнике
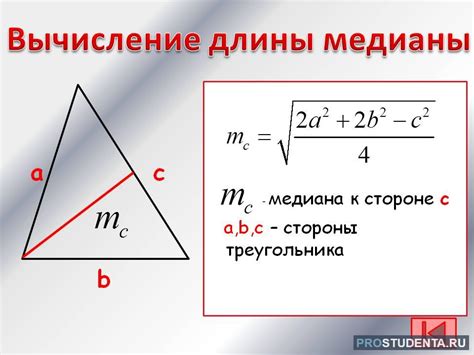
Медиана = (1/2) * √(2 * с^2 + 2 * b^2 - a^2)
где a, b и c - длины катетов и гипотенузы треугольника.
Чтобы рассчитать длину медианы, необходимо знать длины сторон треугольника. Если известна длина гипотенузы и одного из катетов, можно использовать теорему Пифагора для вычисления второго катета. Затем полученные значения вводятся в формулу для расчёта длины медианы.
Допустим, у нас имеется прямоугольный треугольник со сторонами a = 3, b = 4 и c = 5. Рассчитаем длину медианы:
- Вычисляем второй катет по формуле Пифагора: a^2 + b^2 = c^2 → 3^2 + b^2 = 5^2 → 9 + b^2 = 25 → b^2 = 16 → b = 4.
- Подставляем значения в формулу для длины медианы: Медиана = (1/2) * √(2 * 4^2 + 2 * 4^2 - 3^2) = (1/2) * √(32 + 32 - 9) = (1/2) * √(55) ≈ 3.72.
Таким образом, длина медианы в прямоугольном треугольнике со сторонами a = 3, b = 4 и c = 5 равна примерно 3.72.
Что такое медиана в треугольнике
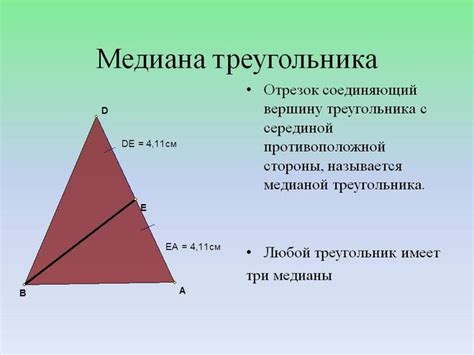
Медиана делит сторону треугольника, к которой она проведена, на две равные части. Также она делит треугольник на две равные площади. Для прямоугольного треугольника медиана, проведенная к гипотенузе, делит ее на две равные части.
Длина медианы в прямоугольном треугольнике может быть найдена с использованием теоремы Пифагора. Если катеты прямоугольного треугольника имеют длины a и b, а гипотенуза имеет длину c, то медиана, проведенная к гипотенузе, имеет длину:
c/2
Таким образом, длина медианы в прямоугольном треугольнике будет равна половине длины гипотенузы.
Существующие методы вычисления медианы в прямоугольном треугольнике
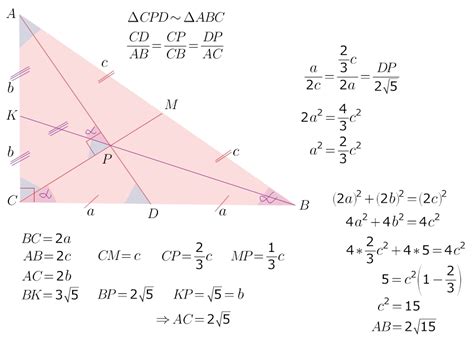
Существует несколько методов вычисления длины медианы в прямоугольном треугольнике:
1. Формула Пифагора. Длина медианы может быть вычислена с использованием теоремы Пифагора. Если a и b - катеты прямоугольного треугольника, а c - гипотенуза, то длина медианы m вычисляется по формуле: m = (2/3) * √(2 * a^2 + 2 * b^2 - c^2).
2. Формулы вычисления длины медианы на основе длин сторон треугольника. Для вычисления длины медианы можно использовать различные формулы, основанные на длинах сторон прямоугольного треугольника. Например, если a и b - катеты, а c - гипотенуза, то длина медианы вычисляется по формуле: m = (√(2a^2 + 2b^2 - c^2))/2.
Выбор метода вычисления медианы в прямоугольном треугольнике зависит от доступных данных и требуемой точности результата. Также следует учитывать, что в прямоугольном треугольнике медиана всегда проходит через вершину прямого угла.
Формула для вычисления длины медианы в прямоугольном треугольнике
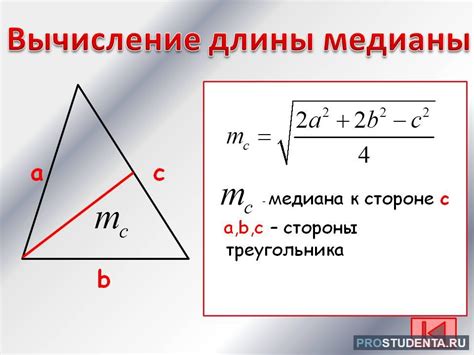
Пусть a и b – катеты прямоугольного треугольника, а c – гипотенуза. Тогда длина медианы m может быть вычислена по следующей формуле:
| m = (sqrt(2 * a^2 + 2 * b^2 - c^2)) / 2 |
Здесь sqrt обозначает извлечение квадратного корня.
Используя данную формулу, можно вычислить длину медианы в прямоугольном треугольнике, зная значения длин его катетов и гипотенузы.
Пример расчёта длины медианы в прямоугольном треугольнике
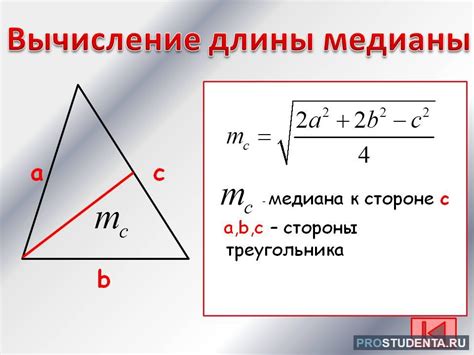
Для расчета длины медианы в прямоугольном треугольнике можно использовать формулу:
Медиана – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
В прямоугольном треугольнике, где один угол равен 90 градусам, медиана, проведенная к гипотенузе, будет равна половине длины гипотенузы.
Рассмотрим пример: у нас есть прямоугольный треугольник ABC, где AC - гипотенуза, а AD - медиана к гипотенузе.
Пусть длина гипотенузы AC равна 10 см. Тогда длина медианы AD будет:
AD = 1/2 * AC = 1/2 * 10 = 5 см.
Таким образом, длина медианы AD в данном примере равна 5 см.
Эту формулу можно использовать для расчета длины медианы в любом прямоугольном треугольнике, зная длину гипотенузы.



