Квадрат, описанный около окружности, представляет собой особый геометрический объект, который обладает рядом интересных свойств. Одно из них – диагональ данного квадрата, которая имеет определенную зависимость от радиуса окружности.
Прежде всего, следует отметить, что описанный квадрат образуется в результате проведения линий, соединяющих все вершины окружности. Данная конструкция является частным случаем описанного квадрата, поскольку каждая сторона этого квадрата касается окружности и его диагонали совпадают с диаметром окружности.
Таким образом, величина диагонали квадрата описанного около окружности равна величине диаметра этой окружности. Диаметр окружности – это отрезок, соединяющий две противоположные точки на окружности и проходящий через ее центр. Радиус, в свою очередь, является половиной диаметра. Поэтому формула для расчета диагонали квадрата, описанного около окружности, выглядит так: диагональ = 2 * радиус.
Диагональ квадрата описанного около окружности: определение и формула
Для расчета длины диагонали квадрата описанного около окружности с известным радиусом окружности или длиной стороны квадрата можно использовать следующую формулу:
- Диагональ квадрата (d) = сторона квадрата (a) * √2
- Диагональ квадрата (d) = 2 * (радиус окружности (r) * √2)
Где √2 - это квадратный корень из двух, приближенное значение которого составляет примерно 1,414.
Например, если известно, что радиус окружности, описывающей квадрат, равен 5 единицам, то диагональ квадрата будет равна 10 * √2 (приближенно 14,14) единиц. А если известна длина стороны квадрата, например, 8 единиц, то диагональ будет равна 8 * √2 (приближенно 11,31) единиц.
Что такое диагональ квадрата описанного около окружности
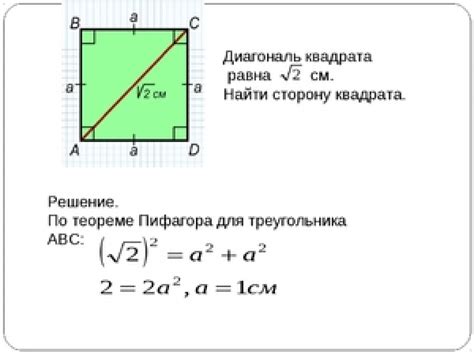
Диагональ является главной линией квадрата и проходит через его центр. Для вычисления длины диагонали квадрата описанного около окружности, можно использовать формулу, основанную на радиусе окружности или на длине стороны квадрата.
Если R обозначает радиус окружности, то длина диагонали D вычисляется следующим образом: D = 2R√2.
Если a обозначает длину стороны квадрата, то длина диагонали D вычисляется так: D = a√2.
Таким образом, диагональ квадрата описанного около окружности является величиной, которая позволяет определить расстояние между двумя противоположными вершинами данного квадрата, а также может быть использована для вычисления других параметров этой геометрической фигуры.
Как найти диагональ квадрата описанного около окружности
Известно, что окружность описанная вокруг квадрата имеет радиус, равный половине диагонали квадрата, а диагональ квадрата равняется удвоенному радиусу окружности. Таким образом, можно сказать, что диагональ квадрата описанного вокруг окружности равна двум радиусам этой окружности.
Для нахождения диагонали квадрата описанного около окружности, необходимо знать радиус этой окружности. Радиус можно найти если известен диаметр или площадь окружности.
Формула для нахождения диагонали квадрата описанного вокруг окружности имеет вид:
диагональ = 2 * радиус
Используя эту формулу, можно легко найти значение диагонали квадрата описанного около окружности, зная ее радиус.