Окружность - это одна из самых фундаментальных фигур в геометрии. Она состоит из всех точек на плоскости, равноудаленных от центра этой окружности. Окружность обладает множеством интересных свойств, одно из которых связано с вписанными углами. В данной статье мы рассмотрим формулу и методы расчета вписанного угла, опирающегося на окружность.
Вписанный угол - это угол, вершина которого расположена на окружности, а стороны - на хорде, считая от концов хорды. Он представляет собой существенную геометрическую концепцию, которая активно используется в различных областях, таких как архитектура, инженерия и физика.
Формула для расчета вписанного угла опирающегося на окружность основана на связи между мерой угла и длиной дуги, выраженной в радианах.
Для нахождения меры вписанного угла необходимо знать меру соответствующей дуги, выраженную в радианах, и радиус окружности. Формула для расчета такого угла выглядит следующим образом: α = l/r, где α - мера вписанного угла в радианах, l - длина дуги окружности, r - радиус окружности.
Вписанные углы имеют множество применений, начиная от научных исследований до применения в повседневной жизни. Они помогают решать разнообразные задачи, например в оптике, где используется закон Снеллиуса, или в аэродинамике, где важно учитывать угол падения и отражения света и звука.
Метод определения вписанных углов на окружности
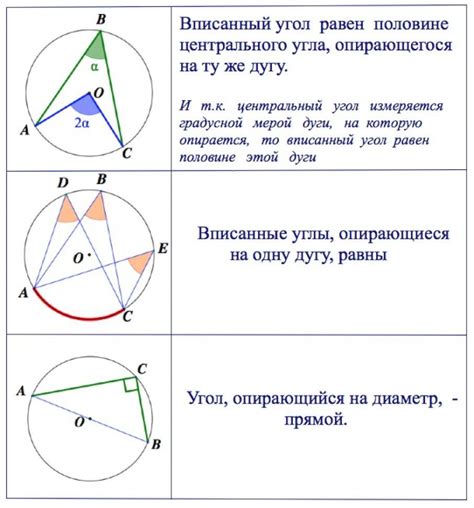
Существует несколько методов определения вписанных углов на окружности, но одним из самых простых и распространенных является использование формулы вписанного угла:
| Формула вписанного угла | Значение |
|---|---|
| Угол между хордами | <ACB |
| Длина хорды AB | c |
| Радиус окружности | r |
| Вписанный угол | 2 * arcsin(c / (2 * r)) |
Для использования этой формулы необходимо знать длину хорды AB и радиус окружности. Сначала вычисляется значение выражения с / (2 * r), затем с помощью обратной функции синуса arcsin получаем вписанный угол.
Метод определения вписанных углов на окружности может быть использован для нахождения не только углов между хордами, но и других вписанных углов, например, углов между касательной к окружности и хордой или углов между хордой и дугой окружности. Знание этого метода позволяет легко решать разнообразные геометрические задачи, связанные с окружностями.
Формула для расчета вписанного угла

Для расчета вписанного угла в окружность необходимо знать длину дуги и радиус окружности. Формула для расчета вписанного угла выглядит следующим образом:
| Формула | Описание |
|---|---|
| α = (s / r) * 180° / π | Угол (α) равен произведению длины дуги (s) на 180°, разделенное на радиус окружности (r) и число Пи (π). |
Здесь:
- α - вписанный угол в градусах;
- s - длина дуги окружности;
- r - радиус окружности.
Данная формула позволяет легко и удобно вычислить вписанный угол в окружность, если известны его основные параметры. Например, если известны длина дуги и радиус окружности, можно с легкостью определить угол, под которым эта дуга будет отображена на окружности.
Как найти величину вписанного угла на основе равномерного распределения точек на окружности
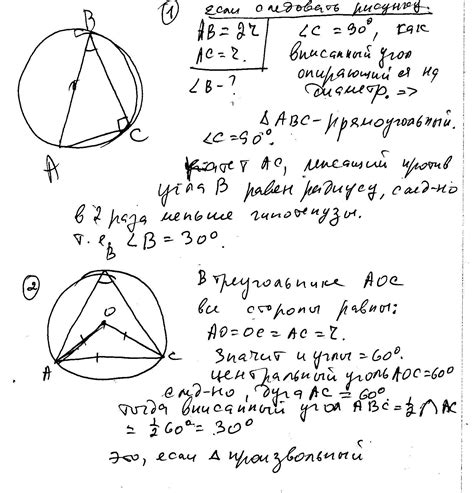
Если точки на окружности равномерно распределены, то можно использовать геометрический метод для нахождения величины вписанного угла.
Предположим, у нас есть окружность радиусом R и n равномерно распределенных точек на этой окружности:
- Вычислим периметр окружности P: P = 2πR.
- Найдем длину дуги между двумя соседними точками: L = P / n.
- Теперь можно найти угол между двумя соседними точками на окружности, используя формулу: α = 360° * (L / 2πR).
Таким образом, мы можем вычислить величину вписанного угла на основе равномерного распределения точек на окружности, используя периметр окружности и количество точек.
Расчет вписанных углов с использованием теоремы о центральном угле
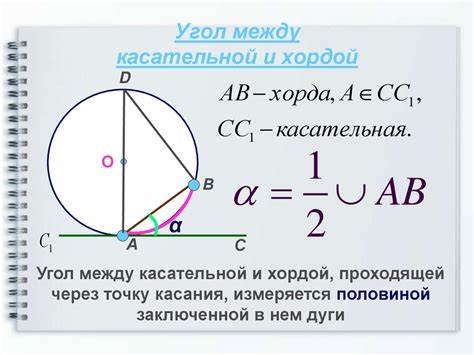
Теорема о центральном угле гласит, что если угол, вписанный в окружность, опирается на дугу, которая равна по длине этой дуге. Другими словами, вписанный угол равен половине центрального угла, соответствующего той же дуге.
Для расчета вписанных углов с использованием теоремы о центральном угле нужно выполнить следующие шаги:
- Определить центральный угол, соответствующий дуге, на которую опирается вписанный угол.
- Рассчитать половину найденного центрального угла.
- Полученное значение будет являться мерой вписанного угла.
Применение теоремы о центральном угле позволяет быстро и точно находить величину вписанного угла, имея информацию о дуге, на которую он опирается. Это особенно полезно при решении задач геометрии или в практических ситуациях, связанных с конструкцией и черчением окружностей.
Как вычислить вписанный угол, если известен радиус окружности и длина дуги
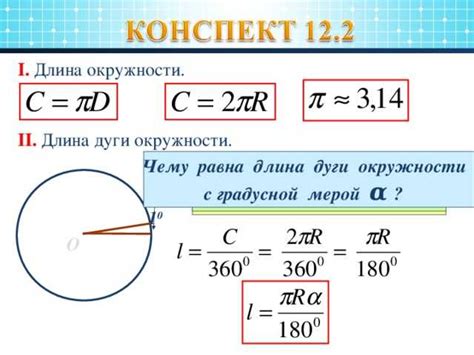
Для вычисления вписанного угла, если известны радиус окружности и длина дуги, можно использовать следующую формулу:
1. Найдите длину окружности, используя формулу C = 2πr, где C - длина окружности, а r - радиус.
2. Выразите вписанный угол, используя формулу θ = (L / C) * 360°, где θ - вписанный угол, L - длина дуги, а C - длина окружности.
Пример вычисления:
- Пусть радиус окружности равен 5 см.
- Найдем длину окружности: C = 2π * 5 = 31.42 см.
- Пусть длина дуги равна 10 см.
- Вычислим вписанный угол: θ = (10 / 31.42) * 360° ≈ 114.6°.
Таким образом, вписанный угол при заданных условиях составляет примерно 114.6°.
Метод нахождения величины вписанного угла по длине хорды и радиусу окружности
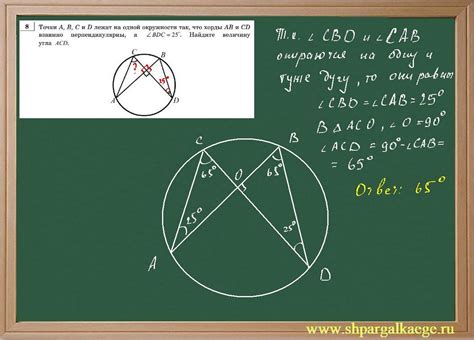
Для нахождения величины вписанного угла, если известны длина хорды и радиус окружности, можно воспользоваться следующей формулой:
- Угол = 2 * arcsin(длина хорды / (2 * радиус окружности))
Данная формула позволяет точно определить величину вписанного угла, зная только длину хорды и радиус окружности. Вписанный угол имеет очень важное значение в геометрии, так как он определяет много других характеристик и свойств фигур, построенных на основе окружности.
Примеры решения задач на расчет вписанных углов
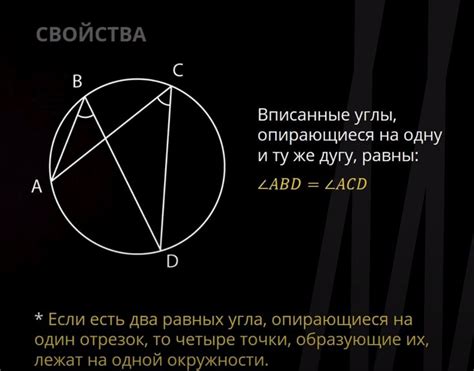
Решение задач на расчет вписанных углов требует применения соответствующих формул и методов. Вот несколько примеров, которые помогут вам понять, как можно решить задачу связанную с вписанным углом:
Пример 1:
Найдите значение вписанного угла A для окружности O, если известно, что мера дуги AB равна 60 градусов.
Решение:
По формуле для вписанных углов, мера вписанного угла равна половине меры дуги. Так как дуга AB равна 60 градусов, то вписанный угол A будет равен 30 градусам.
Пример 2:
Окружность O имеет радиус 5 см. Найдите значение вписанного угла B, если известно, что длина хорды AB равна 8 см.
Решение:
Сначала найдем длину дуги AB по формуле: длина дуги = 2 * радиус * sin(вписанный угол / 2). Подставим известные значения: 8 = 2 * 5 * sin(B / 2).
Решив данное уравнение, получим sin(B / 2) = 8 / 10 = 0.8. Затем найдем вписанный угол B, воспользовавшись обратной функцией синуса: B / 2 = arcsin(0.8), B / 2 ≈ 53.13 градусов. Так как вписанный угол равен половине угла, то B ≈ 106.26 градусов.
Это лишь два примера, которые демонстрируют основные методы решения задач на расчет вписанных углов. В каждой задаче можно использовать соответствующие формулы, в зависимости от известных данных. Важно помнить, что для решения задач данного типа требуется хорошее знание геометрии и алгебры.



