Трапеция - это геометрическая фигура, которая состоит из двух параллельных сторон и двух непараллельных сторон, называемых основаниями. Внутри трапеции можно вписать окружность, которая касается всех сторон данной фигуры. Интересующий нас вопрос состоит в нахождении периметра такой трапеции.
Для решения этой задачи необходимо знать, что вписанная в окружность трапеция обладает таким свойством: сумма длин двух параллельных сторон равна сумме длин двух непараллельных сторон. Из этого следует, что периметр трапеции вписанной в окружность равен сумме длин всех ее сторон.
Пусть основание трапеции обозначается как a, бо́льшее основание - как b, меньшее основание - как c, а боковая сторона - как d. Тогда периметр трапеции равен a + b + c + d.
Таким образом, чтобы найти периметр трапеции вписанной в окружность, необходимо сложить длины всех ее сторон. Ответ на вопрос оказывается очень простым!
Изучаем периметр трапеции в окружности, узнайте формулу
Если a и b - длины параллельных сторон, а R - радиус окружности, то формула для вычисления периметра трапеции в окружности выглядит так:
П = a + b + 2πR
В этой формуле 2πR - длина окружности с радиусом R, а сумма a + b - длина двух параллельных сторон трапеции.
Таким образом, зная радиус и длины параллельных сторон, можно легко вычислить периметр трапеции в окружности по данной формуле.
Помните, что периметр - это важный параметр фигуры, который позволяет определить её размер и форму.
Трапеция вписанная в окружность: определение и свойства
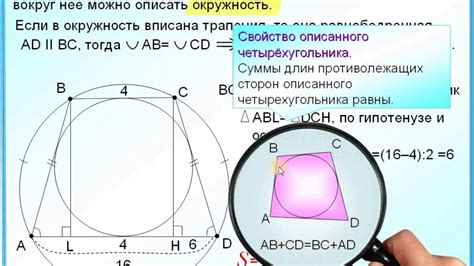
Трапеция вписанная в окружность обладает следующими свойствами:
| Стороны трапеции | Стороны трапеции являются хордами окружности, соединяющими вершины трапеции. Длины хорд можно найти, используя теорему косинусов или теорему синусов. |
| Диагонали трапеции | Диагонали трапеции являются хордами окружности, пересекающимися внутри окружности. Длины диагоналей можно найти, используя теорему Пифагора. |
| Углы трапеции | Углы трапеции могут быть разделены на две группы: основные углы и вершины углы. Основные углы являются прилежащими к основаниям трапеции и сумма их всегда равна 180 градусов. Вершины углы являются противоположными и сумма каждой пары вершиных углов также равна 180 градусов. |
| Периметр трапеции | Периметр трапеции вписанной в окружность можно найти, сложив длины всех четырех ее сторон. Если стороны трапеции известны, то периметр можно найти с помощью простой формулы. |
Трапеция вписанная в окружность имеет много интересных свойств и является объектом исследования в геометрии. Это всего лишь некоторые из свойств этой фигуры.
Формула для вычисления периметра вписанной трапеции
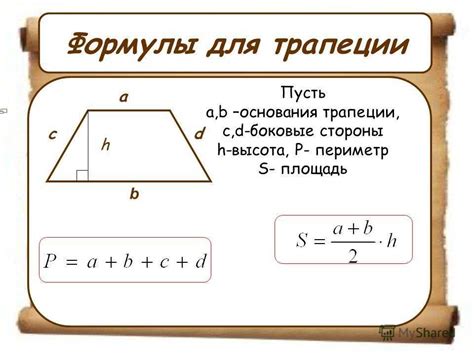
Периметр = a + b + c + d
где:
- a - длина одного основания трапеции
- b - длина другого основания трапеции
- c - длина боковой стороны трапеции
- d - длина боковой стороны трапеции
Учтите, что в вписанной трапеции стороны равны друг другу попарно: a = b и c = d. Поэтому формулу периметра можно упростить:
Периметр = a + b + c + d = a + a + c + c = 2a + 2c
Таким образом, формула для вычисления периметра вписанной трапеции может быть представлена как:
Периметр = 2a + 2c
Как найти радиус окружности вписанной в трапецию
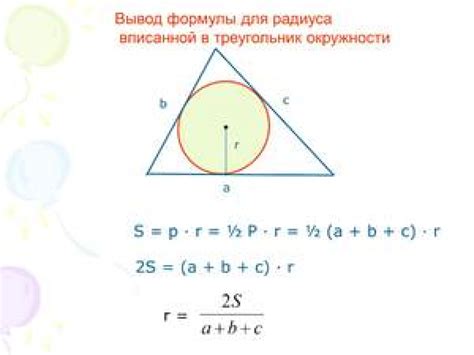
Чтобы найти радиус окружности, вписанной в трапецию, необходимо знать длины боковых сторон трапеции и её оснований.
Для рассмотрения данной задачи используем следующие обозначения:
AB и CD - основания трапеции.
BC и AD - боковые стороны трапеции.
O - центр окружности, вписанной в трапецию.
r - радиус окружности.
Также известно, что радиус окружности, вписанной в трапецию, является перпендикуляром к её основаниям AB и CD.
Сначала найдём сумму оснований трапеции AB и CD:
| AB + CD | ||||
| BC - AD |
Образуется выражение, которое представляет собой отношение суммы оснований к разности боковых сторон:
(AB + CD) / (BC - AD) = 2 * r
Далее находим радиус окружности, используя полученное выражение:
r = (AB + CD) / (2 * (BC - AD))
Таким образом, зная длины оснований и боковых сторон трапеции, можно легко найти радиус окружности, вписанной в неё.
Решение задачи: нахождение периметра и радиуса трапеции вписанной в окружность
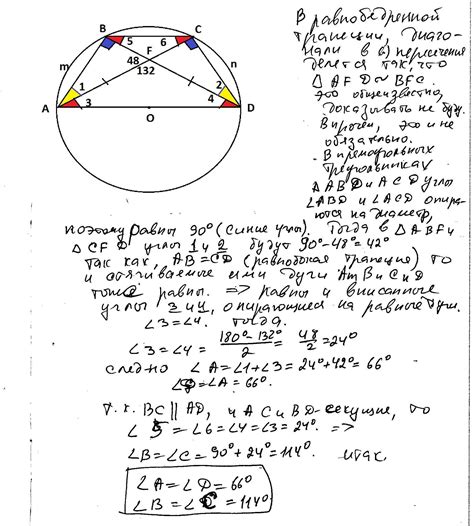
Периметр трапеции равен сумме длин всех ее сторон. Для нахождения периметра вписанной трапеции можно воспользоваться следующей формулой:
Периметр = 2r + a + b
где r - радиус окружности, a и b - длины оснований трапеции.
Радиус окружности, вписанной в трапецию, можно найти, зная длины ее оснований и высоту. Высоту трапеции можно найти по теореме Пифагора:
h = √(a^2 - b^2)
где h - высота трапеции.
Теперь, зная длины оснований и высоту, можно вычислить радиус окружности по формуле:
r = h/2
Таким образом, используя найденное значение радиуса, можно вычислить периметр вписанной трапеции по формуле, описанной выше.



