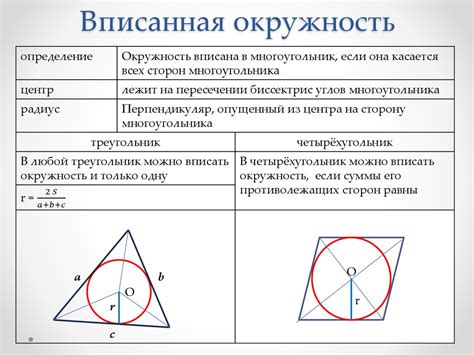
Вписанная окружность - это окружность, которая касается всех сторон многоугольника, а описанная окружность - это окружность, которая проходит через все вершины многоугольника.
Вписанная окружность является особенностью многоугольника и всегда имеет центр внутри фигуры. Такая окружность касается каждой стороны многоугольника только в одной точке. Вписанная окружность имеет ряд полезных свойств, которые используются в геометрии. Например, длина радиуса вписанной окружности связана с данными ограничениями и размерами многоугольника.
Описанная окружность, напротив, проходит через все вершины многоугольника и расположена снаружи фигуры. Центр описанной окружности находится на пересечении серединных перпендикуляров к сторонам многоугольника. Радиус oписанной окружности равен половине диагонали вписанного многоугольника.
Важно отметить, что вписанная и описанная окружности имеют взаимосвязь. Радиус вписанной окружности можно найти, зная радиус описанной окружности и наоборот. Кроме того, вписанная и описанная окружности используются в различных математических задачах и формулах.
Что такое вписанная и описанная окружности?
Вписанная окружность - это окружность, которая полностью помещается внутри фигуры и касается всех её сторон. То есть, её центр лежит внутри фигуры, а радиус равен расстоянию от центра до любой стороны фигуры. Например, для треугольника вписанная окружность касается всех его сторон.
Описанная окружность - это окружность, которая полностью охватывает фигуру и касается всех её вершин. То есть, она проходит через все вершины фигуры, а её центр находится на перпендикуляре, проходящем через середины сторон фигуры. Например, для треугольника описанная окружность проходит через все его вершины.
Вписанная и описанная окружности имеют много интересных свойств и связей с фигурами, с которыми они связаны. Изучение этих окружностей позволяет более глубоко понять геометрию фигур и решать различные задачи, связанные с ними.
Определение вписанной окружности
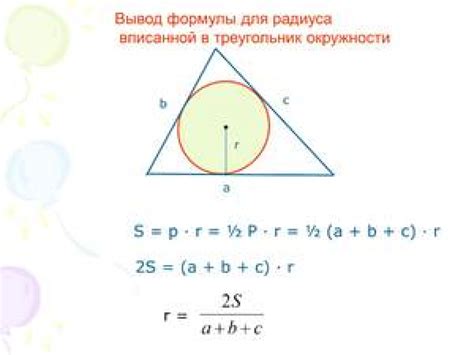
Вписанная окружность имеет следующие свойства:
- Центр вписанной окружности находится внутри многоугольника.
- Радиус вписанной окружности равен половине длины стороны, к которой она касается.
- Вписанная окружность касается всех сторон многоугольника в единственной точке каждой стороны.
- Сумма длин отрезков, проведенных от вершин многоугольника до точек касания вписанной окружности, равна периметру многоугольника.
Вписанная окружность играет важную роль в геометрии. Она имеет много применений, включая построение и изучение треугольников, нахождение площади и периметра многоугольников, а также в решении задач на нахождение углов и расстояний.
Определение описанной окружности
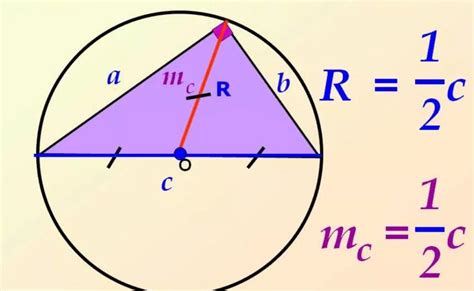
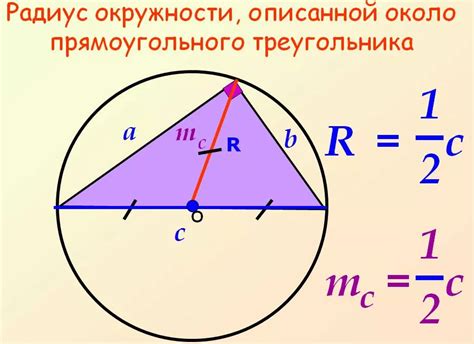
Для того чтобы построить описанную окружность, нужно знать радиус и центр окружности. Центр описанной окружности лежит на перпендикулярных биссектрисах всех трех углов треугольника. Радиус описанной окружности равен половине длины стороны треугольника, деленной на синус угла треугольника.
Описанная окружность играет важную роль в геометрии и обладает рядом свойств. Например, для прямоугольного треугольника, описанная окружность совпадает с гипотенузой и имеет свойство быть диаметром его окружности. Также, описанная окружность является тангенциальной к серединным перпендикулярам сторон треугольника и косвенно влияет на расчеты в задачах геометрии.
| Свойство | Описанная окружность |
|---|---|
| Центр окружности | Лежит на перпендикулярных биссектрисах углов треугольника |
| Радиус окружности | Равен половине длины стороны треугольника, деленной на синус угла треугольника |
| Свойство для прямоугольного треугольника | Описанная окружность совпадает с гипотенузой и является диаметром |
| Тангенциальность | Является тангенциальной к серединным перпендикулярам сторон треугольника |
Отличия между вписанной и описанной окружностями
Вписанная окружность - это окружность, которая полностью лежит внутри данной фигуры и касается всех её сторон. Если речь идет о треугольнике, то вписанная окружность проходит через вершины треугольника и касается всех его сторон.
Описанная окружность - это окружность, которая проходит через все вершины данной фигуры. Описанная окружность треугольника касается всех его сторон, а описанная окружность четырехугольника - касается всех его сторон и диагоналей.
Диаметры вписанной и описанной окружностей взаимно перпендикулярны. Другими словами, отрезки, соединяющие центр окружности с точками касания, перпендикулярны к соответствующим сторонам фигуры.
Вписанная окружность имеет меньший радиус, чем описанная окружность. Так как вписанная окружность полностью лежит внутри фигуры, её радиус должен быть меньше радиуса описанной окружности.



