В геометрии, симметрия - это способность фигуры оставаться неизменной при определенных преобразованиях. Два из наиболее распространенных типов симметрии - осевая и центральная. Они играют важную роль в разных областях науки, и отличаются основными принципами.
Осевая симметрия, также известная как зеркальная, является наиболее простым типом симметрии. Здесь фигура сохраняет свою форму и размеры при отражении относительно невидимой линии, называемой осью симметрии. Примерами могут служить слово, которое может быть прочитано одинаково справа налево и слева направо, или изображение, которое можно сложить пополам и получить одинаковые половинки.
Центральная симметрия более сложна и интересна. Здесь фигура сохраняет свою форму и размеры при вращении вокруг точки, называемой центром симметрии. Каждая точка на фигуре имеет парную точку, расположенную на равном удалении от центра симметрии, но в противоположном направлении. Примерами могут служить радиальные рисунки, многоугольники, орнаменты и многие другие объекты, которые выглядят одинаково в любом расположении относительно их центра.
Центральная симметрия и осевая симметрия: основные различия
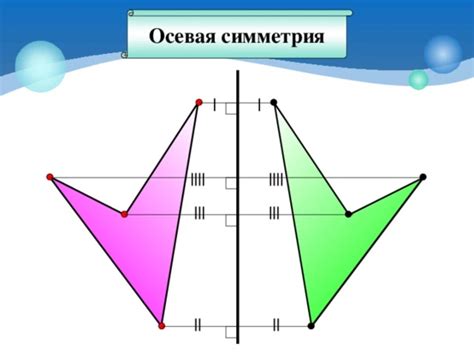
Центральная симметрия является типом симметрии, при котором объект симметричен относительно определенной точки, называемой центром симметрии. Если провести прямую линию через центр симметрии и каждую точку, симметричную симметричной через эту линию, то получится идентичное изображение. Примерами центральной симметрии могут служить круги и окружности, а также многие другие геометрические фигуры.
Осевая симметрия включает в себя симметрию симметрии вокруг оси, при которой объекты симметричны относительно оси. Объекты, обладающие осевой симметрией, могут быть перевернуты вокруг оси на 180 градусов, чтобы получить их идентичное изображение. Примерами осевой симметрии являются равнобедренные треугольники и буквы, такие как "А" или "М".
Основное различие между центральной симметрией и осевой симметрией заключается в том, что центральная симметрия осуществляется относительно точки, в то время как осевая симметрия осуществляется относительно оси.
Центральная симметрия и осевая симметрия являются важными концепциями не только в геометрии, но и в многих других областях, таких как изобразительное искусство и дизайн. Понимание и применение этих типов симметрии помогает создавать гармоничные и эстетически привлекательные композиции.
Общие понятия и определения

Осевая симметрия – это тип симметрии, при котором фигура может быть разделена на две одинаковые половины с помощью прямой, называемой осью симметрии. Осевая симметрия встречается часто в природе, например, в форме лица или ветвей деревьев. В математике, осевая симметрия отображает фигуру на себя, сохраняя ее форму и размеры.
Центральная симметрия – это тип симметрии, при котором фигура может быть разделена на две симметричные части относительно определенной точки, называемой центром симметрии. Центральная симметрия также встречается в различных объектах и узорах, как в природе, так и в искусстве. В математике, центральная симметрия отображает фигуру на себя, меняя только направление и относительное положение.
Важно отметить, что осевая симметрия может иметь больше одной оси симметрии, в то время как центральная симметрия всегда имеет только один центр симметрии. Также осевая симметрия может быть не полной, то есть фигура может быть симметричной только относительно определенных точек или линий, в то время как центральная симметрия всегда является полной.
Кроме того, осевая симметрия часто относится к двумерным фигурам, таким как геометрические фигуры или буквы, в то время как центральная симметрия может быть применена к более широкому спектру объектов и форм, включая трехмерные объекты.
Таким образом, центральная симметрия и осевая симметрия представляют собой разные типы симметрии, каждый из которых обладает своими характеристиками и принципами, но оба играют важную роль в математике, искусстве и природе.
Центральная симметрия: основные характеристики
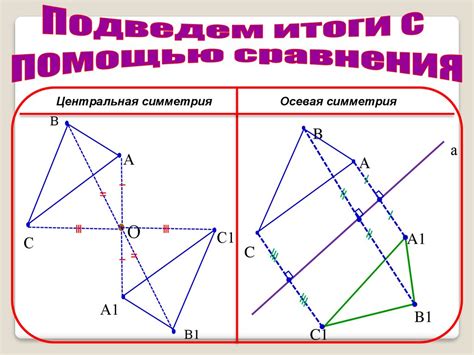
Центральная симметрия основана на понятии центра симметрии – точки, относительно которой выполняется отражение объектов. В результате отражения каждая точка плоскости переходит в такую же точку, но с обратным направлением вектора радиуса, соединяющего центр симметрии с этой точкой.
Центральная симметрия имеет следующие основные характеристики:
- Относительно центра симметрии выполняется бесконечное количество отражений.
- Если точка находится на линии симметрии, то ее отражение совпадает с исходной точкой.
- Линии симметрии в центральной симметрии – это все прямые, проходящие через центр симметрии.
- Фигуры, симметричные относительно точки или линии симметрии, называются симметричными фигурами.
- Центр симметрии может находиться как внутри фигуры, так и снаружи нее.
Центральная симметрия широко используется в геометрии, а также в различных областях науки и искусства, где требуется создание сбалансированного и гармоничного дизайна.
Осевая симметрия: особенности и примеры
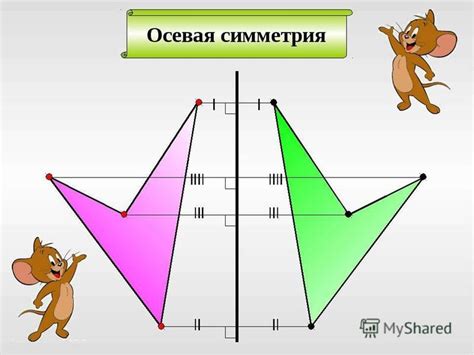
Осевая симметрия имеет несколько особенностей:
- Ось симметрии должна быть прямой. При этом прямая может быть вертикальной, горизонтальной или даже наклонной.
- Каждая точка объекта находится на одинаковом расстоянии от оси симметрии. Это означает, что если мы измерим расстояние от исходной точки до оси, оно будет равно расстоянию от симметричной точки до этой же оси.
- Осевая симметрия применима к разным объектам, например, к геометрическим фигурам, буквам алфавита, растениям и т.д.
Примеры объектов с осевой симметрией:
| Объект | Ось симметрии |
| Круг | Любая прямая, проходящая через его центр |
| Прямоугольник | Любая вертикальная или горизонтальная прямая, проходящая через его центр |
| Буква "А" | Вертикальная прямая, проходящая посередине буквы |
| Растишка | Линия, проходящая посередине стебля |



