Целые точки в графиках функции – это особые точки на графике, которые имеют целочисленные координаты. В математике они играют важную роль, поскольку помогают нам понять поведение функции и ее свойства. Целые точки могут быть как минимальными, так и максимальными значениями функции на определенном интервале, а также точками, в которых функция принимает целочисленное значение.
Целые точки в графиках функции могут иметь различную природу. Например, они могут быть точками, в которых функция достигает максимального или минимального значения на заданном интервале. В этом случае целые точки помогают нам определить экстремумы функции и понять, где она наиболее или наименее выражена.
Кроме того, целые точки на графике могут быть также точками пересечения функции с осями координат. Например, при решении уравнения функции мы ищем ее корни, которые представляют собой целочисленные значения. Эти корни будут являться целыми точками на графике и помогут нам понять, где функция пересекает ось абсцисс или ординат.
Целые точки в графиках функции: определение и примеры
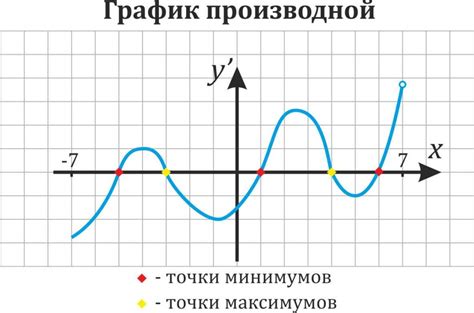
Для определения целых точек в графиках функции необходимо рассмотреть значения аргумента и значения функции при этих значениях аргумента. Если оба значения являются целыми числами, то точка на графике с такими координатами будет целой точкой.
Рассмотрим пример функции y = 2x + 1. Подставляя различные целые значения аргумента x, мы можем получить целые значения функции y. Например, при x = 0, y = 1, что означает, что точка (0, 1) является целой точкой на графике функции. Аналогично, индуцируя другие целые значения аргумента, мы можем получить другие целые точки на графике.
Целые точки в графиках функции могут иметь важное значение в различных областях математики и естествознания. Они могут помочь в выявлении закономерностей и установлении зависимостей между переменными. Кроме того, целые точки могут использоваться для построения графиков с высокой степенью точности и детализации.
Что такое целые точки в графиках функции
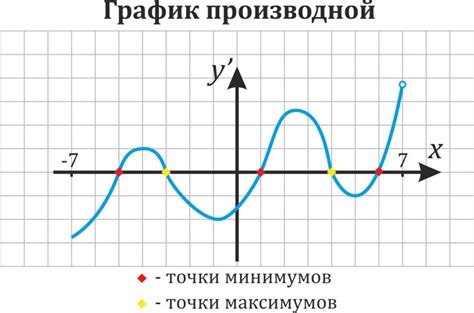
Целые точки могут быть важными для анализа функции и ее свойств. Иногда целые точки могут предоставить информацию о характеристиках функции, таких как симметрия, экстремумы или пересечения с осями координат.
Примером может служить функция y = sin(x), которая имеет целую точку при x = 0, где и значение функции, и значение аргумента являются целыми числами.
Целые точки в графиках функции могут играть важную роль в анализе и понимании свойств функций, поэтому их определение и исследование являются важными аспектами изучения математики.
Как определить целые точки
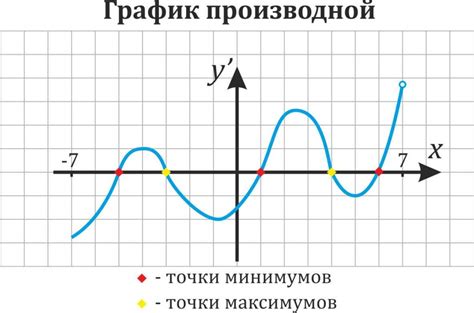
Для примера рассмотрим функцию f(x) = x^2 - 3x + 2. Чтобы определить целые точки данной функции, подставим значения целых чисел в уравнение и проверим результат:
| x | f(x) |
|---|---|
| 0 | 2 |
| 1 | 0 |
| 2 | 2 |
Таким образом, точки (0, 2) и (2, 2) являются целыми точками функции f(x) = x^2 - 3x + 2.
Определение целых точек в графиках функций позволяет исследовать их свойства, находить точки пересечения с осями координат, а также проводить анализ поведения функции на разных участках графика.
Примеры целых точек в графиках функции
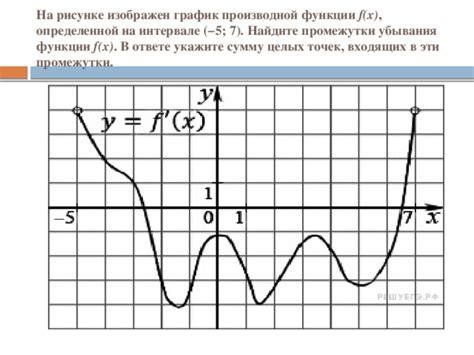
Целые точки в графиках функции могут иметь особую значимость при анализе и понимании свойств функций. Вот несколько примеров целых точек в графиках функции:
| Функция | Целые точки | Описание |
|---|---|---|
| y = x | (0,0), (1,1), (-1,-1), ... | Данная функция представляет собой прямую линию, проходящую через начало координат. Все точки с целочисленными координатами лежат на этой линии. |
| y = x^2 | (0,0), (1,1), (-1,1), ... | Эта функция является параболой с вершиной в точке (0,0). Все точки с целочисленными координатами находятся на этой параболе или на оси симметрии. |
| y = sin(x) | (0,0), (π,0), (-π,0), ... | Функция синуса имеет периодичность 2π и проходит через ноль в целочисленных значениях аргумента. Следовательно, на графике можно наблюдать целочисленные точки на оси абсцисс. |
Это лишь некоторые примеры целых точек в графиках функции. Важно отметить, что наличие целых точек может зависеть от выбора диапазона значений для аргумента функции.
Значение целых точек для анализа графика
Изучение целых точек позволяет определить особенности графика функции и выявить особые значения, которые могут иметь физический или математический смысл.
Неравенства, экстремумы и пересечения с осями координат – все это можно выявить, анализируя график функции в целых точках.
Например, если график функции пересекает ось абсцисс в целой точке, то это означает, что значение функции равно нулю в этой точке. Это может указывать на наличие корня уравнения, решение которого ищется.
Целые точки на графиках функции могут также указывать на периодичность, симметрию или другие свойства функции. Изучение этих точек помогает установить закономерности и понять поведение функции на всем протяжении области определения.
Таким образом, значение целых точек в анализе графиков функций помогает раскрыть множество интересных и полезных свойств функции, а также предоставляет возможность более глубокого понимания ее поведения и структуры.
Связь целых точек с другими характеристиками функции
Целые точки на графике функции имеют важное значение и могут быть связаны с другими характеристиками самой функции. Эти точки могут являться максимумами, минимумами или перегибами функции.
Целое число точек называется максимумом функции, если оно является наибольшим значением функции на некотором интервале. Максимумы часто обозначаются как точки, где график функции имеет вершины.
Целому числу точек называется минимумом функции, если оно является наименьшим значением функции на некотором интервале. Минимумы часто обозначаются как точки, где график функции имеет впадины.
Целое число точек может быть перегибом функции, если функция меняет выпуклость или вогнутость графика в данной точке. Перегибы могут быть связаны с изменением знака второй производной функции или сменой кривизны графика.
Целые точки на графике функции являются важными характеристиками и могут помочь в анализе поведения функции и определении ее свойств. Изучение этих характеристик может помочь понять форму графика функции и принять правильные решения при решении математических задач.



