Частное от деления - одно из основных понятий в математике, которое позволяет определить результат деления одного числа на другое. Часто встречающийся символ для обозначения частного от деления - это обратная косая черта (/). Оно указывает на то, что число, расположенное перед ней, является числителем и будет делиться на число, расположенное после нее, которое является знаменателем.
Частное от деления может быть как целым числом, так и десятичной дробью. Целочисленное частное от деления - это результат, когда при делении двух чисел целая часть полученной дроби равна нулю. Например, если мы разделим число 15 на 5, то получим целочисленное частное от деления - число 3. Десятичная дробь - это результат, когда при делении двух чисел целая часть полученной дроби больше нуля.
Частное от деления имеет свои свойства, среди которых можно выделить следующие: единица делится на любое число и даёт в результате это число; ноль не делится на никакое число и даёт в результате ноль (кроме случая, когда число является бесконечностью); произведение частного от деления и делителя всегда равно делимому. Знание определения и свойств частного от деления позволит более глубоко разобраться в математических аспектах деления и успешно применять их на практике.
Частное от деления

Частное от деления может быть представлено в виде десятичной дроби или обыкновенной дроби, в зависимости от типа исходных чисел. Если частное представлено в виде десятичной дроби, то это означает, что деление не является точным, и результата можно приблизительно выразить со степенью точности.
Пример:
Делимое: 15
Делитель: 3
Частное: 5
В данном примере, число 15 содержит в себе число 3 пять раз. Таким образом, частное от деления равно 5.
Определение и понятие

Чтобы найти частное от деления, нужно разделить делимое число на делитель. Часто в математике используется обозначение ":", "/", или символ дроби для обозначения деления.
Например, если мы разделим число 10 на число 2, то получим 5. Здесь 10 - делимое, 2 - делитель, а 5 - частное от деления.
Другой пример: при делении числа 15 на число 3, получаем частное 5. То есть 15 : 3 = 5.
Особенностью частного от деления без остатка является то, что оно всегда будет целым числом. Если результат деления имеет дробную часть, она будет отброшена и останется только целая часть.
Как найти частное от деления?

Для того, чтобы найти частное от деления, нужно выполнить следующие шаги:
- Запишите делимое и делитель.
- Выполните деление одного числа на другое.
- Результатом деления будет частное.
Например, если мы хотим найти частное от деления числа 10 на число 2, то записываем:
| Делимое: | 10 |
| Делитель: | 2 |
Делаем деление:
| 10 ÷ 2 = 5 |
В результате получаем, что частное от деления числа 10 на число 2 равно 5.
Частное от деления может быть как целым числом, так и десятичной дробью.
Например, если мы хотим найти частное от деления числа 7 на число 3, то записываем:
| Делимое: | 7 |
| Делитель: | 3 |
Делаем деление:
| 7 ÷ 3 = 2.33 |
В результате получаем, что частное от деления числа 7 на число 3 равно 2.33 (округленное до двух знаков после запятой).
Таким образом, нахождение частного от деления является важной частью арифметики и позволяет нам определить, сколько раз одно число содержится в другом.
Что такое остаток от деления?

Остаток от деления обозначается символом "%", например, 12 % 5 = 2, где 12 - делимое, 5 - делитель, а 2 - остаток.
Остаток от деления очень полезен при решении различных задач. Например, он может использоваться для определения четности или нечетности числа, для нахождения остатка от деления больших чисел, для вычисления периодической десятичной дроби и т.д.
Остаток от деления можно использовать в различных областях математики, физики, программирования и других науках.
Примеры частного от деления в математике
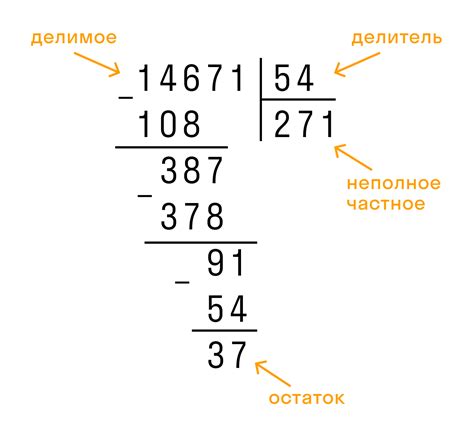
Вот некоторые примеры частного от деления:
- 10 / 2 = 5. В этом примере число 10 делится на число 2, и результатом является число 5.
- 20 / 4 = 5. В этом примере число 20 делится на число 4, и результатом также является число 5.
- 15 / 3 = 5. В этом примере число 15 делится на число 3, и результатом снова является число 5.
Частное от деления может быть как целым числом, так и дробным числом. Если результат деления является целым числом, то говорят, что деление является без остатка, например, 10 / 2 = 5.
Однако, если результат деления является дробным числом, то говорят, что деление имеет остаток. Например, 10 / 3 = 3.33333333333 и так далее. В этом случае остаток от деления равен 1.
Частное от деления играет важную роль в математике и используется в различных областях, например, в физике, экономике и программировании. Это позволяет нам делить числа и вычислять результаты математических операций.
Зачем нужно находить частное от деления?

Первое применение нахождения частного от деления - это вычисление доли или долей от целого. Например, если у вас есть 10 яблок и нужно поделить их поровну между 2 детьми, то частное от деления будет равно 5. Таким образом, каждый ребенок получит по 5 яблок.
Второе применение частного от деления - это вычисление среднего значения или среднего арифметического. Например, если у вас есть 4 оценки за предмет и вы хотите найти средний балл, можно сложить оценки и разделить полученную сумму на 4, чтобы получить частное от деления. Таким образом, вы найдете средний балл.
Третье применение - это нахождение коэффициента пропорциональности. Например, если у вас есть два числа, и вы хотите найти коэффициент пропорциональности, можно поделить одно число на другое, чтобы получить частное от деления, и таким образом найти коэффициент пропорциональности.
Таким образом, нахождение частного от деления является важным математическим понятием, которое имеет множество практических применений и используется в различных сферах деятельности.



