Биссектриса угла – это особый элемент геометрической фигуры, который проходит через вершину угла и делит его на два равных угла. Такой элемент имеет большое значение в геометрии, так как позволяет решать различные задачи, связанные с углами и треугольниками.
Главное свойство биссектрисы угла заключается в том, что она делит угол пополам, то есть образует смежные углы, равные между собой. Отсюда следует, что биссектриса угла является прямой. Зная эту особенность, можно с помощью биссектрисы угла находить различные значения и равенства углов, а также строить треугольники по заданным условиям.
Например, если нам необходимо найти угол, равный данному углу, мы можем провести биссектрису и получить два равных угла. Затем, измерив один из них, мы сможем определить величину искомого угла.
Знание биссектрисы угла играет важную роль в решении задач на построение треугольников и вычисление значений углов. Это основополагающий элемент геометрии, который позволяет анализировать и работать с углами, а также делает решение геометрических задач более простым и понятным.
Определение биссектрисы угла
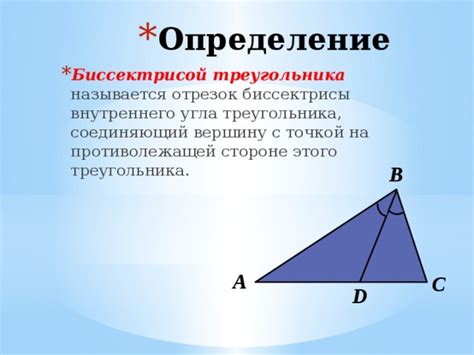
Для определения биссектрисы угла можно использовать циркуль и линейку. Сначала рисуется данная нам вершина угла, затем с помощью циркуля проводятся дуги с одинаковым радиусом из этой вершины. После этого проводится линия, которая соединяет вершину угла с точками пересечения дуг. Таким образом, получается биссектриса угла.
Биссектриса угла обладает следующими свойствами:
- Биссектриса угла всегда проходит через его вершину.
- Биссектриса угла делит данный угол на два равных угла.
Биссектриса угла имеет большое значение в геометрии, так как она позволяет находить точку пересечения углов и проводить различные угловые построения.
Расчет биссектрисы угла
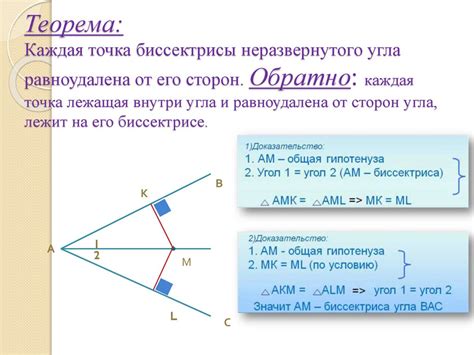
- Измерьте величину заданного угла с помощью транспортира.
- Разделите величину измеренного угла на 2.
- Отложите полученную величину от начала угла внутрь угла.
- Проведите луч от начала угла через отложенную точку. Этот луч будет являться биссектрисой данного угла.
Таким образом, вы сможете найти биссектрису угла либо с помощью ручного расчета, либо с помощью графического построения. Расчет биссектрисы угла является важным элементом геометрии и позволяет вычислить точку, в которой биссектриса пересекается с противоположной стороной угла.
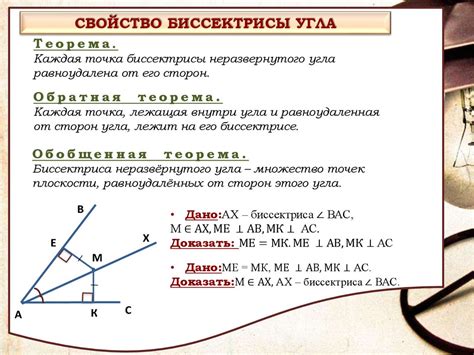
Свойства биссектрисы угла
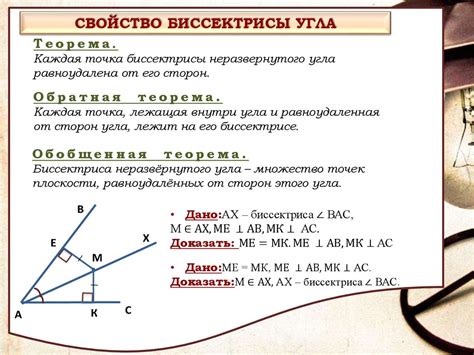
Основные свойства биссектрисы угла:
- Разделение угла на два равных угла: Биссектриса делит исходный угол на два равных угла. Это значит, что полуразмахи, образованные биссектрисой и одной из сторон угла, равны между собой.
- Перпендикулярное пересечение: Биссектриса угла пересекает противоположную сторону угла перпендикулярно. То есть, если мы проведем прямую через точку пересечения биссектрисы и противоположной стороны, она будет перпендикулярна к этой стороне.
- Пропорциональное деление сторон: Биссектриса угла делит противоположные стороны этого угла пропорционально их длине. Если сторона AB делится биссектрисой угла A на отрезки AC и BC, то отношение длин отрезков AC и BC равно отношению длин сторон AB и AB противоположного угла.
- Взаимное положение биссектрис: Биссектрисы двух углов, образованных пересекающимися прямыми, взаимно перпендикулярны. То есть, если две прямые пересекаются под определенным углом, то их биссектрисы образуют сегменты этого угла, которые взаимно перпендикулярны.
Эти свойства биссектрисы угла являются основой для решения различных задач в геометрии.
Геометрическое представление биссектрисы угла
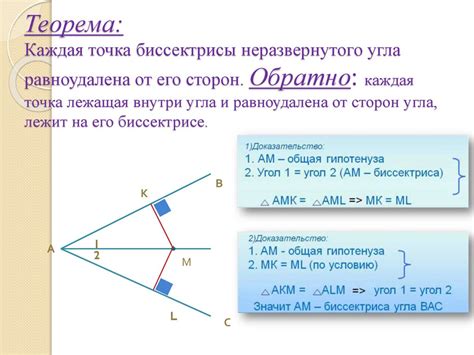
Первый способ
С помощью компаса и линейки биссектрису угла можно построить следующим образом:
- На линейке откладываем отрезок, равный отрезку одного из сторон угла.
- Ставим точку на каждом конце отрезка.
- С помощью компаса делаем метку на линейке, соединяющей данные точки.
- Проводим линию через точку на углу и точку деления на линейке.
Второй способ
С использованием угломера можно построить биссектрису угла следующим образом:
- Накладываем угломер на вершину угла так, чтобы одна из его сторон лежала на одной из сторон угла.
- Проводим линию с помощью угломера, соединяющую вершину угла и любую точку на одной из сторон угла.
- Проводим линию, проходящую через вершину угла и середину отрезка, соединяющего угол и точку на одной из его сторон.
Используя данные методы, можно геометрически представить биссектрису угла и получить линию, делящую исходный угол пополам.
Применение биссектрисы угла
1. Решение геометрических задач. Биссектриса угла используется для нахождения равных частей угла и решения задач, связанных с расчетом угловых величин. Например, если мы знаем одну часть биссектрисы и знаем, что угол делится на две равные части, мы можем найти длину другой части биссектрисы и решить задачу.
2. Построение перпендикуляров и угловых биссектрис. Биссектриса угла часто используется при построении перпендикуляров и угловых биссектрис в геометрии. Это позволяет строить перпендикулярные линии и находить серединный угол в полукруге или полуокружности.
3. Разделение углов в многоугольниках. Биссектрисы углов часто используются для деления углов в многоугольниках на равные части. Например, при нахождении среднего угла в треугольнике или замерами углов в пятиугольнике для определения, является ли он правильным.
4. Измерение углов в ежедневной жизни. Биссектриса угла часто используется для измерения углов в различных ситуациях в ежедневной жизни. Например, при определении угла наклона скатов крыши при строительстве или измерении углов при установке мебели в квартире.
Таким образом, понимание и применение биссектрисы угла в геометрии и повседневной жизни позволяет нам решать различные задачи, связанные с расчетом и измерением углов, построением перпендикуляров и делением углов в многоугольниках.
Примеры решения задач с использованием биссектрисы угла
Рассмотрим несколько примеров задач, в которых требуется найти длину биссектрисы угла.
Пример 1:
Дан треугольник ABC, в котором известны длины сторон AB = 5 см, BC = 7 см и AC = 9 см. Найдите длину биссектрисы угла B.
| Решение: |
|---|
| 1. Воспользуемся формулой для нахождения длины биссектрисы угла B: |
| BL = (AC * BA) / (AC + AB) = (9 * 5) / (9 + 5) = 45 / 14 ≈ 3.21 см |
| 2. Ответ: длина биссектрисы угла B равна примерно 3.21 см. |
Пример 2:
Дан треугольник PQR, в котором известны длины сторон PQ = 8 см, QR = 10 см и PR = 12 см. Найдите длину биссектрисы угла Q.
| Решение: |
|---|
| 1. Воспользуемся формулой для нахождения длины биссектрисы угла Q: |
| QM = (PR * PQ) / (PR + PQ) = (12 * 8) / (12 + 8) = 96 / 20 = 4.8 см |
| 2. Ответ: длина биссектрисы угла Q равна 4.8 см. |
Таким образом, биссектриса угла - это линия, которая делит данный угол на два равных угла. Для нахождения длины биссектрисы угла можно использовать соответствующую формулу, которую можно легко применить в решении различных геометрических задач.



