Бинарные отношения - одна из важнейших концепций в дискретной математике, изучающей объекты счетного характера. Они позволяют описывать связи и взаимосвязи между элементами различных множеств и являются основой для решения множества задач в таких областях, как теория графов, компьютерные науки и математическая логика.
Бинарное отношение представляет собой подмножество декартова произведения двух множеств. Оно описывает наличие или отсутствие связи между элементами этих множеств. Каждый элемент пары из декартова произведения называется упорядоченной парой и имеет вид (a, b), где a - элемент первого множества, b - элемент второго множества.
Такие отношения могут быть рефлексивными (когда каждый элемент множества находится в отношении с самим собой), симметричными (когда каждая упорядоченная пара имеет свою обратную пару) или транзитивными (когда для любых трех элементов (a, b), (b, c), (a, c) отношения выполнено (a, c)). На базе этих базовых свойств строятся различные операции с бинарными отношениями, такие как объединение, пересечение и дополнение.
Определение бинарных отношений в дискретной математике
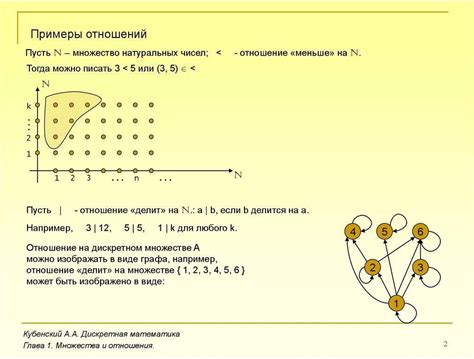
Бинарные отношения представляют собой важный инструмент в дискретной математике, позволяющий анализировать связи и взаимодействия между элементами в множествах. В математической терминологии бинарное отношение между двумя множествами A и B определяется как подмножество A × B, где A × B обозначает декартово произведение множеств A и B.
Другими словами, бинарное отношение R между множествами A и B задается парами элементов из A и B. Каждая такая пара (a, b), где a принадлежит A, а b принадлежит B, является участником отношения R.
Для более точного определения отношения R между A и B можно использовать альтернативную запись, в которой участвуют три множества: A, B и R. В этом случае отношение R представляет собой подмножество A × B и записывается в виде R ⊆ A × B.
Бинарные отношения могут быть различных типов, включая отношения эквивалентности, порядка и функциональные отношения. Они играют важную роль в различных областях, включая логику, теорию графов и компьютерные науки, и широко применяются для анализа и моделирования различных систем.
Понятие бинарного отношения и его роль в дискретной математике

В дискретной математике бинарное отношение играет ключевую роль, являясь одним из основных понятий. Оно обладает большой значимостью в различных областях, таких как логика, теория графов, алгебра и другие.
Бинарное отношение – это связь между двумя множествами, которая определяет, какие элементы первого множества связаны с элементами второго. Формально, бинарное отношение R на множестве A × B определяется как подмножество кросс-произведения множеств A и B.
Важно отметить, что бинарные отношения могут быть разных типов: рефлексивными, симметричными, транзитивными и т.д. Каждый тип связан с определенными свойствами отношения и играет свою роль в дискретной математике.
Бинарные отношения широко используются в теории графов, где множество вершин и ребер задает отношение между ними. Они также находят применение в логике, где множество пропозиций и логических связок задает отношение между пропозициями.
Изучение бинарных отношений позволяет анализировать и описывать различные взаимосвязи в системах и структурах. Они позволяют рассматривать элементы и их связи с другими элементами, что дает инструмент для изучения множественных отношений и понимания их свойств.
В итоге, понятие бинарного отношения и его роль в дискретной математике являются основополагающими для понимания и исследования различных математических структур и систем. Они являются фундаментом для множества важных концепций и методов, используемых в дискретной математике.
Примеры бинарных отношений в реальной жизни

Бинарные отношения представляют собой инструмент, который помогает нам анализировать сравнительные характеристики между двумя элементами или объектами в реальном мире. Ниже приведены некоторые примеры бинарных отношений и их применение в повседневной жизни:
1. Отношение "быть членом": Это отношение используется для определения, является ли один объект членом другого объекта. Например, можно определить, является ли человек членом какой-либо организации или клуба.
2. Отношение "быть меньше или равным": Это отношение используется для сравнения чисел и определения, является ли одно число меньшим или равным другому. Например, можно сравнить два возраста, чтобы определить, кто из них старше или моложе.
3. Отношение "быть родителем": Это отношение используется для определения родительства между двумя объектами. Например, можно определить, является ли один человек родителем другого.
4. Отношение "быть соседом": Это отношение используется для определения, находятся ли два объекта рядом друг с другом. Например, можно определить, являются ли два дома соседними друг к другу.
5. Отношение "быть предшественником": Это отношение используется для определения порядка между двумя объектами. Например, можно определить, какие числа идут перед или после другого числа.
Все эти примеры бинарных отношений помогают нам лучше понять и анализировать связи и сравнения между объектами в реальной жизни. Они играют важную роль в решении проблем и принятии решений в различных сферах, таких как организации, математика, социология и т. д.
Важные свойства бинарных отношений

Существуют несколько важных свойств, которыми обладают бинарные отношения:
1. Рефлексивность: Бинарное отношение R на множестве A называется рефлексивным, если для каждого элемента a из A выполняется условие (a, a) принадлежит R. Иными словами, каждый элемент множества A связан с самим собой.
2. Симметричность: Бинарное отношение R на множестве A называется симметричным, если для любых элементов a и b из A, если (a, b) принадлежит R, то (b, a) также принадлежит R. То есть, если элемент a связан с элементом b, то элемент b также связан с элементом a.
3. Антисимметричность: Бинарное отношение R на множестве A называется антисимметричным, если для любых элементов a и b из A, если (a, b) и (b, a) принадлежат R, то a равно b. То есть, если элемент a связан с элементом b и элемент b связан с элементом a, то a равно b.
4. Транзитивность: Бинарное отношение R на множестве A называется транзитивным, если для любых элементов a, b и c из A, если (a, b) и (b, c) принадлежат R, то (a, c) тоже принадлежит R. То есть, если элемент a связан с элементом b и элемент b связан с элементом c, то элемент a также связан с элементом c.
Знание этих свойств позволяет анализировать и классифицировать бинарные отношения, а также использовать их в решении различных задач и проблем.
Классификация бинарных отношений в дискретной математике
Бинарные отношения могут быть классифицированы в соответствии с различными критериями. Рассмотрим некоторые из них:
| Классификация | Описание |
|---|---|
| Рефлексивное отношение | Если каждый элемент множества связан сам с собой, то отношение является рефлексивным. Например, отношение "больше или равно" для чисел. |
| Антирефлексивное отношение | Если ни один элемент множества не связан сам с собой, то отношение антирефлексивное. Например, отношение "меньше" для чисел. |
| Симметричное отношение | Если для каждой пары элементов (a, b) из множества, если (a, b) связано, то (b, a) также связано, то отношение является симметричным. Например, отношение "равно" для чисел. |
| Антисимметричное отношение | Если для каждой пары различных элементов (a, b) из множества, если (a, b) связано, то (b, a) не связано, то отношение является антисимметричным. Например, отношение "меньше или равно" для чисел. |
| Транзитивное отношение | Если для каждой тройки элементов (a, b, c) из множества, если (a, b) и (b, c) связаны, то (a, c) также связано, то отношение является транзитивным. Например, отношение "меньше" для чисел. |
| Антитранзитивное отношение | Если для каждой тройки различных элементов (a, b, c) из множества, если (a, b) и (b, c) связаны, то (a, c) не связано, то отношение является антитранзитивным. Например, отношение "больше" для чисел. |
Эти классификации бинарных отношений помогают нам лучше понимать и анализировать отношения между элементами различных множеств, и применять их в различных математических моделях и приложениях.



