Асимптота - это важное понятие в математике, которое используется для описания поведения функции при стремлении аргумента к бесконечности или к некоторому другому значению. Она является своего рода границей или пределом функции. Понимание асимптоты помогает анализировать и описывать сложные функции и их поведение в различных точках.
Для поиска асимптоты функции необходимо выполнить определенные шаги. Во-первых, рассмотреть экстремумы функции и ее поведение при стремлении аргумента к бесконечности. Если функция имеет горизонтальную асимптоту, то при стремлении аргумента к бесконечности, функция будет переходить к определенному значению на оси ординат.
Во-вторых, необходимо исследовать вертикальные асимптоты. Если функция имеет вертикальную асимптоту, то при стремлении аргумента к определенному значению, функция будет стремиться к плюс или минус бесконечности.
Что такое асимптота?
Горизонтальная асимптота обозначается уравнением y = c, где c - постоянное значение. Она представляет собой горизонтальную прямую, к которой график функции стремится, когда x стремится к бесконечности или минус бесконечности.
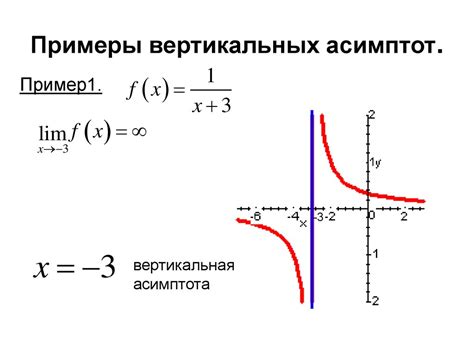
Вертикальная асимптота обозначается уравнением x = c, где c - постоянное значение. Она представляет собой вертикальную прямую, к которой график функции стремится, когда x приближается к конкретному значению, но не достигает его.
Наклонная асимптота - это прямая линия, которая приближается к графику функции и имеет угол наклона. Уравнение наклонной асимптоты имеет вид y = mx + b, где m - наклон, а b - смещение по вертикали.
Для нахождения асимптот необходимо анализировать поведение функции на бесконечностях, наличие разрывов и особенностей, а также проводить дополнительные вычисления, если это требуется.
Зачем нужно знать асимптоту?

Знание асимптоты позволяет нам также более эффективно работать с функциями и вычислять их значение. Например, при применении методов численного интегрирования, знание асимптоты позволяет нам выбрать наиболее оптимальный метод и упростить вычисления. Аналогично, при решении уравнений и систем уравнений, знание асимптоты может помочь нам найти более точное и быстрое решение.
И наконец, знание асимптоты позволяет нам лучше понять и описать сложные математические объекты. Например, асимптоты могут помочь нам определить тип и классификацию функций, их границы и ограничения. Они также могут помочь нам описать геометрическую форму функции и ее связи с другими функциями и фигурами.
Анализ функций

Асимптоты - это прямые или кривые, которые приближаются к графику функции, но никогда не пересекают его. Асимптоты могут быть горизонтальными, вертикальными или наклонными.
Чтобы найти асимптоты функции, необходимо исследовать ее поведение на бесконечности. Для этого вычисляют предел функции при стремлении аргумента к бесконечности или минус бесконечности. Если предел существует и конечен, то функция имеет асимптоту. В зависимости от значения предела, можно определить тип асимптоты.
Горизонтальная асимптота обозначает горизонтальную линию, которая бесконечно приближается к графику функции на бесконечности. Предельное значение функции равно значению горизонтальной асимптоты. Функция может иметь одну или несколько горизонтальных асимптот на разных интервалах.
Вертикальная асимптота представляет собой вертикальную прямую, которая приближается к графику функции на бесконечности. Она определяется значением аргумента, при котором функция стремится к бесконечности или минус бесконечности. Функция может иметь несколько вертикальных асимптот в различных точках.
Наклонная асимптота представляет собой прямую, которая приближается к графику функции на бесконечности и имеет угол наклона. Прямая задается уравнением y = mx + b, где m - наклон асимптоты, b - точка пересечения с осью ординат. Функция может иметь одну или несколько наклонных асимптот.
Анализ функций и нахождение их асимптот помогает понять поведение графиков функций, выявить особенности и свойства функций, и решать задачи с использованием асимптот. Этот процесс является важной частью математического анализа и используется в разных областях, таких как физика, экономика и инженерия.
Как найти горизонтальную асимптоту?
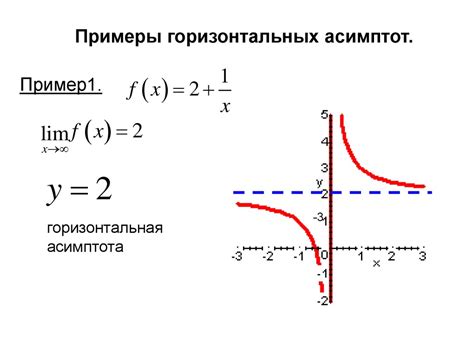
Чтобы найти горизонтальную асимптоту, необходимо выполнить следующие шаги:
- Определить предел функции при стремлении аргумента к положительной бесконечности.
- Определить предел функции при стремлении аргумента к отрицательной бесконечности.
Если эти пределы существуют и равны, то график функции имеет горизонтальную асимптоту. Значение этого предела и является координатой горизонтальной асимптоты.
Для нахождения пределов функции можно использовать методы анализа пределов, такие как правила Лопиталя или правила замены переменной.
Например, рассмотрим функцию f(x) = (3x^2 + 2x + 1) / (4x^2 + 5x + 2). Чтобы найти горизонтальную асимптоту этой функции, необходимо вычислить пределы функции f(x) при x стремящемся к положительной и отрицательной бесконечности. Если эти пределы существуют и равны, то график функции имеет горизонтальную асимптоту на данном участке.
Определение горизонтальной асимптоты позволяет лучше понять поведение функции на бесконечности и использовать эту информацию при построении графика функции или решении задачи, связанной с функцией.
Как найти вертикальную асимптоту?
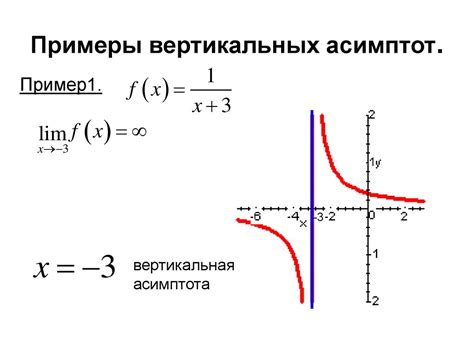
Когда мы ищем вертикальную асимптоту, мы ищем значения аргумента, при которых функция имеет бесконечную величину или не существует. Существует несколько способов найти вертикальную асимптоту:
- Анализируем выражение функции. Если в выражении функции присутствуют дроби, то вертикальная асимптота может возникнуть там, где знаменатель обращается в ноль.
- Решаем уравнение, приравнивая знаменатель функции к нулю. Найденное значение будет являться x-координатой вертикальной асимптоты.
- Вычисляем значения функции при значении аргумента, приближающемся к найденной x-координате вертикальной асимптоты. Если функция стремится к бесконечности или не существует при этом значении, то это будет вертикальная асимптота.
Обратите внимание, что при наличии вертикальной асимптоты в функции, график функции будет иметь промежутки разрыва. Одна сторона графика будет приближаться к вертикальной асимптоте, а другая сторона будет отдаляться от нее.
Примеры применения

1. Техническая физика:
Асимптоты применяются в технической физике для описания поведения систем в предельных случаях. Например, в электронике асимптотические линии используются для анализа и проектирования фильтров и усилителей. Асимптоты также используются при моделировании и анализе механических систем, таких как колебания и качения.
2. Математическая анализ:
Асимптоты применяются в математическом анализе для описания поведения функций вблизи бесконечности или вблизи некоторой точки. Например, асимптоты используются для определения предельных значений функций, нахождения асимптотического разложения функций или вычисления интегралов.
3. Графическое искусство:
Асимптоты применяются в графическом искусстве, особенно в архитектуре и дизайне, для создания гармоничных композиций и планирования пространства. Например, в архитектуре асимптотические линии используются для создания перспективных рисунков или проектирования фасадов зданий. В дизайне асимптотические кривые используются для создания плавных и симметричных форм.
Асимптоты находят применение в различных областях, где требуется анализ функций, описание поведения систем или создание гармоничных композиций. Изучение асимптот помогает лучше понять и описать сложные явления и визуализировать важные аспекты моделей и систем.
Асимптотическая сложность алгоритмов

Существует несколько видов асимптотической сложности: константная сложность (O(1)), логарифмическая сложность (O(log n)), линейная сложность (O(n)), и т.д. Каждый из этих видов сложности описывает, как меняется время работы алгоритма в зависимости от размера входных данных.
Одним из способов определить асимптотическую сложность алгоритма является анализ его кода и вычисление количества операций, которые он выполняет. Затем, используя математическую нотацию «O-нотации», можно представить эту сложность в виде символического выражения, где буква O означает «оценка» или «порядок».
Например, если алгоритм выполняет одну операцию независимо от размера входных данных, его сложность будет константной и обозначаться как O(1). Если же алгоритм выполняет количество операций, пропорциональное логарифму от размера входных данных, его сложность будет логарифмической и обозначаться как O(log n).
Знание асимптотической сложности алгоритмов очень полезно при выборе наиболее оптимального решения задачи. Оно помогает определить, какой алгоритм будет работать быстрее и занимать меньше памяти, и позволяет сделать осознанный выбор между различными реализациями.
Асимптотическое поведение функций

При изучении асимптотического поведения функций можно выделить несколько случаев:
- Горизонтальная асимптота. Если функция стремится к постоянному значению при приближении аргумента к бесконечности, то говорят, что у функции есть горизонтальная асимптота. Горизонтальная асимптота задается уравнением вида y = c, где c - постоянное значение.
- Вертикальная асимптота. Если функция стремится к бесконечности или такому значению, которое бесконечности очень близко, то говорят, что у функции есть вертикальная асимптота. Вертикальная асимптота задается уравнением вида x = a, где a - константа.
- Наклонная асимптота. Если функция приближается к прямой линии, но не является ни горизонтальной, ни вертикальной асимптотой, то говорят, что у функции есть наклонная асимптота. Наклонная асимптота задается уравнением вида y = mx + b, где m и b - константы.
Определение и поиск асимптот функции важны для анализа ее поведения и для понимания ее глобального тренда. При определении асимптоты нужно учитывать ограничения функции, возможность бесконечного приближения и другие условия, которые могут влиять на ее поведение в пределе. Точное определение асимптот требует применения математических методов и инструментов, таких как пределы и производные функций.



