Арифметические действия с десятичными дробями – это основные операции, которые можно выполнять над числами с десятичной частью. Десятичные дроби – это числа, которые представляют собой целую часть и десятичную часть, разделенные запятой или точкой. В отличие от обычных целых чисел, десятичные дроби позволяют работать с более точными значениями и более точно оценивать результаты арифметических операций.
Арифметические действия с десятичными дробями включают сложение, вычитание, умножение и деление. Однако, перед тем как начать выполнять эти операции, необходимо убедиться в правильном понимании десятичной системы счисления и правилах округления чисел. Также, при выполнении арифметических действий с десятичными дробями, необходимо учитывать порядок операций и приоритетность операций, чтобы получить корректный результат.
Арифметические действия с десятичными дробями могут быть полезны при решении различных задач, таких как вычисление скидок, расчет долей и процентов, а также во многих других областях, где требуется точное вычисление дробных значений. Понимание основных правил и приемов арифметики с десятичными дробями позволяет осуществлять точные и эффективные вычисления, что очень важно в современном мире, где математика является неотъемлемой частью многих сфер жизнедеятельности.
Что такое арифметические действия

Сложение - это операция, при которой два числа складываются вместе. Результат сложения называется суммой. Например, 2 + 3 = 5.
Вычитание - это операция, при которой из одного числа вычитается другое число. Результат вычитания называется разностью. Например, 5 - 3 = 2.
Умножение - это операция, при которой два числа перемножаются. Результат умножения называется произведением. Например, 2 * 3 = 6.
Деление - это операция, при которой одно число делится на другое число. Результат деления называется частным. Например, 6 / 3 = 2.
Арифметические действия могут выполняться с разными типами чисел, включая целые числа, десятичные числа и дроби. Они являются основой для решения математических задач и использования в повседневной жизни.
Основные операции с десятичными дробями

Сложение десятичных дробей проводится путем сложения целых частей и десятичных частей отдельно. Сначала складываются целые части, а затем десятичные части. Если сумма десятичных частей превышает единицу, переносится единица на целую часть.
Вычитание десятичных дробей также осуществляется поэтапно. Первым шагом проводится вычитание десятичных частей и, при необходимости, заем одной единицы. Затем вычитается целая часть и, если нужно, еще одна единица занимается из целой части предыдущего числа.
Умножение двух десятичных дробей проводится путем перемножения целых частей и десятичных частей отдельно. Затем произведения складываются, и полученная сумма десятичная записывается после запятой.
Деление двух десятичных дробей производится аналогично делению целых чисел, но дополнительно учитывается наличие десятичных частей. Целая часть делимого делится на целую часть делителя, а десятичная часть делимого делится на десятичную часть делителя. Затем полученные результаты складываются.
Основные операции с десятичными дробями являются важным элементом математического образования и используются в решении различных задач. Понимание этих операций позволяет эффективно работать с десятичными числами и проводить точные вычисления.
Сложение десятичных дробей

Сложение десятичных дробей представляет собой процесс объединения двух или более десятичных дробей в одну сумму. Для выполнения операции сложения десятичных дробей необходимо следовать определенным правилам.
1. Выравнивание знаков перед запятой. Перед сложением десятичных дробей необходимо выровнять их знаки перед запятой, чтобы запятые во всех дробях находились на одной позиции.
2. Сложение целых частей. Если дроби имеют целую часть, они сначала складываются как обычные числа. Целые части суммируются, а дробные части остаются без изменений.
3. Сложение дробных частей. После сложения целых частей, дробные части каждой дроби складываются по отдельности. Запятая в результате помещается на ту же позицию, что и в исходных дробях.
4. Упрощение результата. Если возможно, полученная сумма может быть упрощена, сокращена или приведена к наименьшему знаменателю.
Процесс сложения десятичных дробей может быть выполнен как вручную, так и с использованием калькуляторов или компьютерных программ. Однако, понимание правил и основных принципов сложения десятичных дробей позволяет легче понять результат и проверить его правильность.
Вычитание десятичных дробей

Для выполнения вычитания десятичных дробей необходимо:
- Выровнять дробные части чисел, добавив нули справа до одинакового количества знаков после запятой.
- Выполнить вычитание дробных частей чисел, а затем вычитание целых частей.
- Упростить полученную разность, если это возможно.
Приведем пример вычитания десятичных дробей:
Дано: 4.58 - 1.23
Выровняем дробные части чисел, добавив нули: 4.580 - 1.230
Выполним вычитание дробных частей: 4.580 - 1.230 = 3.350
Выполним вычитание целых частей: 4 - 1 = 3
Таким образом, разность между 4.58 и 1.23 равна 3.35.
Вычитание десятичных дробей может быть применено в различных ситуациях, например, при решении задач по финансам или в ежедневных расчетах. Важно правильно выравнивать дробные части чисел и аккуратно выполнять вычитание, чтобы получить точный и правильный результат.
Умножение десятичных дробей

Для умножения десятичных дробей нужно выполнить следующие шаги:
- Умножить числитель первой дроби на числитель второй дроби. Это даст числитель произведения.
- Умножить знаменатель первой дроби на знаменатель второй дроби. Это даст знаменатель произведения.
- Полученный числитель и знаменатель составляют произведение десятичных дробей.
Пример:
Умножить десятичные дроби 0,3 и 0,5.
- 0,3 * 0,5 = 0,15
Таким образом, произведение десятичных дробей 0,3 и 0,5 равно 0,15.
Умножение десятичных дробей может быть полезным при решении задач, связанных с долями, процентами, финансами и другими областями, где требуется точность до десятых или сотых.
Деление десятичных дробей

Для выполнения деления десятичных дробей необходимо выравнять число знаков после запятой, так чтобы количество знаков после запятой в делимом и делителе совпадало. Затем дробь делимого делим на дробь делителя.
При делении десятичных дробей может возникнуть необходимость в округлении результата. Обычно результат округляется до определенного количества знаков после запятой в зависимости от требуемой точности.
При делении десятичных дробей также можно использовать различные методы упрощения дробей, например, сокращение общих множителей или упрощение выражения в десятичную дробь.
Деление десятичных дробей широко применяется в финансовой и экономической сферах, при расчетах процентных ставок, валютных операциях, расчетах налогов и прочих финансовых операциях. Точность деления десятичных дробей играет важную роль при выполнении точных расчетов и принятии правильных решений.
Важно помнить, что деление десятичных дробей может привести к получению периодической или бесконечной десятичной дроби. В таких случаях рекомендуется использовать специальные методы или обозначения для записи и работы с такими числами.
Примеры арифметических действий с десятичными дробями

Арифметические действия с десятичными дробями осуществляются так же, как и с обыкновенными числами. Рассмотрим несколько примеров, чтобы понять, как происходят эти действия.
Пример 1:
| Дано: | 0.7 + 0.3 |
| Решение: | 0.7 + 0.3 = 1.0 |
| Ответ: | 1.0 |
Пример 2:
| Дано: | 0.4 - 0.1 |
| Решение: | 0.4 - 0.1 = 0.3 |
| Ответ: | 0.3 |
Пример 3:
| Дано: | 0.6 * 0.2 |
| Решение: | 0.6 * 0.2 = 0.12 |
| Ответ: | 0.12 |
Пример 4:
| Дано: | 0.8 / 0.4 |
| Решение: | 0.8 / 0.4 = 2.0 |
| Ответ: | 2.0 |
Пример 5:
| Дано: | 0.25 + 0.75 - 0.5 |
| Решение: | 0.25 + 0.75 - 0.5 = 0.5 |
| Ответ: | 0.5 |
Таким образом, арифметические действия с десятичными дробями выполняются по тем же правилам, что и с обыкновенными числами.
Пример сложения десятичных дробей
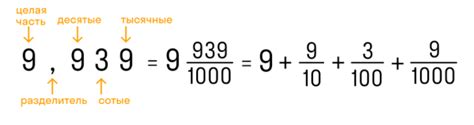
Приведем пример сложения двух десятичных дробей:
Пример:
0,25 + 0,75
Шаг 1: Составляем дроби с общим знаменателем. В данном примере общий знаменатель равен 100, так как у обоих дробей знаменатель равен 4. Для этого умножим каждую дробь на 25:
0,25 * 100 = 25
0,75 * 100 = 75
Шаг 2: Складываем числители дробей:
25 + 75 = 100
Шаг 3: Получаем сумму дроби, разделив полученное число на общий знаменатель:
100 / 100 = 1
Ответ: 0,25 + 0,75 = 1
Таким образом, результат сложения двух десятичных дробей равен 1.
Пример вычитания десятичных дробей

Предположим, у нас есть две десятичные дроби: 0.7 и 0.3. Мы хотим найти разность между ними. Чтобы выполнить это вычитание, мы можем выровнять десятичные разряды, чтобы разряды после запятой находились в одной позиции. В данном случае, так как у нас только один разряд после запятой, это уже выполнено.
Теперь мы можем вычесть разряды после запятой друг из друга: 7 - 3 = 4. Полученное число 4 будет разрядом после запятой в ответе.
Далее, мы вычитаем разряды до запятой: 0 - 0 = 0. Полученное число 0 будет разрядом до запятой в ответе.
Таким образом, разность двух десятичных дробей 0.7 и 0.3 равна 0.4.



