Алгоритм Евклида - это один из первых и самых простых алгоритмов, используемых для нахождения наибольшего общего делителя (НОД) двух чисел. Этот алгоритм был разработан древнегреческим математиком Евклидом около 300 года до нашей эры и с тех пор широко используется в математике и информатике.
Алгоритм Евклида основан на простой идее: наибольший общий делитель двух чисел равен наибольшему общему делителю остатка от деления первого числа на второе и второго числа на остаток. Другими словами, если мы имеем два числа a и b и a > b, то НОД(a, b) равен НОД(b, a % b), где % обозначает операцию взятия остатка.
Алгоритм Евклида можно представить в виде следующей последовательности шагов:
- Если второе число равно 0, то НОД первого числа и второго числа равен первому числу.
- В противном случае, необходимо найти остаток от деления первого числа на второе число.
- Затем необходимо заменить первое число на второе число, а второе число на остаток.
- Повторить шаги 1-3, пока второе число не станет равным 0.
Алгоритм Евклида является очень эффективным способом нахождения НОД, так как он работает за время O(log n), где n - меньшее из двух чисел. Этот алгоритм широко применяется в различных областях, включая криптографию, теорию чисел, компьютерную графику и даже в компьютерных играх.
Алгоритм Евклида для нахождения наибольшего общего делителя (НОД)
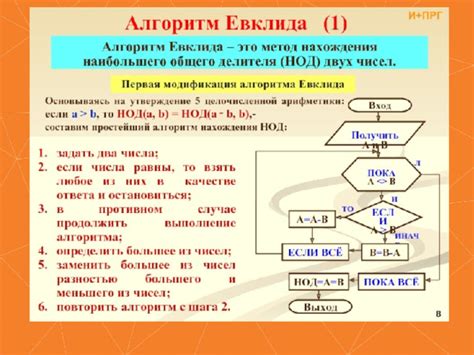
Работа алгоритма Евклида основана на принципе: если a и b - два числа, где a >= b, то НОД(a, b) = НОД(b, a mod b), где mod - операция получения остатка от деления.
Для применения алгоритма Евклида необходимо повторять итерации, пока b не станет равным 0. Когда это произойдет, a будет являться НОДом.
Давайте рассмотрим пример:
Пусть у нас есть числа a = 48 и b = 18. Применяя алгоритм Евклида, мы можем увидеть следующие шаги:
Шаг 1: НОД(48, 18) = НОД(18, 48 mod 18) = НОД(18, 12)
Шаг 2: НОД(18, 12) = НОД(12, 18 mod 12) = НОД(12, 6)
Шаг 3: НОД(12, 6) = НОД(6, 12 mod 6) = НОД(6, 0)
Шаг 4: НОД(6, 0) = 6
Таким образом, наш НОД равен 6.
Алгоритм Евклида является одним из самых эффективных способов нахождения НОД двух чисел. Он применим в различных областях, включая криптографию, алгебру и программирование.
Принцип работы алгоритма Евклида
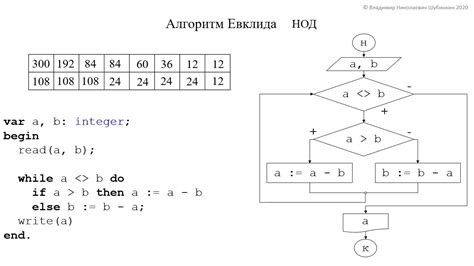
Пусть у нас есть два числа a и b, и мы хотим найти их НОД с помощью алгоритма Евклида. Сначала мы проверяем, является ли одно из чисел a или b нулем. Если это так, то НОД равен ненулевому числу. Если оба числа ненулевые, мы повторяем следующие действия:
- Если a больше b, вычитаем b из a и присваиваем результат a.
- Если b больше a, вычитаем a из b и присваиваем результат b.
- Повторяем шаги 1 и 2, пока a и b не станут равными.
Когда a и b становятся равными, их значение является искомым НОД. Это происходит потому, что при каждой итерации алгоритма одно из чисел уменьшается, а другое остается неизменным, пока они не станут равными. Итоговое число, равное НОД, будет являться самым большим общим делителем исходных чисел.
Алгоритм Евклида обладает высокой эффективностью и может быть применен для нахождения НОД даже для очень больших чисел. Он широко используется в математике, криптографии, алгоритмах сортировки и других областях.
Как использовать алгоритм Евклида для нахождения НОД?

Для применения алгоритма Евклида для нахождения НОД следует следующий процесс:
- Выбираем два числа, для которых нужно найти НОД.
- Вычисляем остаток от деления большего числа на меньшее число. Если остаток равен нулю, то меньшее число является НОД.
- Иначе, записываем остаток и обновляем большее число как меньшее число, а меньшее число как остаток от деления.
- Повторяем шаги 2 и 3 до тех пор, пока не получим остаток равный нулю.
- Последнее ненулевое число будет являться НОДом для исходных чисел.
Преимущество алгоритма Евклида заключается в его простоте и эффективности. За счет способа выбора остатков он позволяет быстро находить НОД даже для очень больших чисел.
Таким образом, алгоритм Евклида является надежным и универсальным инструментом для нахождения НОД двух чисел и широко используется в различных алгоритмических задачах и математических вычислениях.
Алгоритм Евклида и его эффективность

Алгоритм Евклида начинается с двух заданных чисел, которые мы обозначим как a и b. Затем производится деление a на b, результат записывается как r (остаток от деления). Если r равен 0, то b является НОДом для a и b. Если r не равен 0, то a заменяется на b, b заменяется на r, и процесс повторяется с новыми значениями a и b.
Алгоритм Евклида является очень эффективным методом нахождения НОД. Он имеет линейную сложность, то есть время выполнения алгоритма пропорционально размеру входных данных. Это делает его одним из самых быстрых алгоритмов для решения этой задачи.
Алгоритм также обладает рядом полезных свойств. Он инвариантен относительно порядка чисел, то есть НОД(a, b) всегда равен НОД(b, a). Он также может быть применен к более чем двум числам путем многократного применения алгоритма к парам чисел.
Благодаря своей простоте и эффективности, алгоритм Евклида широко применяется в разных областях, включая криптографию, компьютерную алгебру и информационную безопасность. Он также является основой для других алгоритмов, таких как расширенный алгоритм Евклида и алгоритм быстрого возведения в степень.
Примеры использования алгоритма Евклида для нахождения НОД

Пример 1:
Для нахождения НОД чисел 24 и 36, применим алгоритм Евклида:
- Делим 36 на 24 и получаем остаток 12.
- Затем делим 24 на 12 и получаем остаток 0.
- Так как остаток равен 0, то НОД чисел 24 и 36 равен последнему ненулевому остатку, т.е. 12.
Пример 2:
Для нахождения НОД чисел 48 и 60, применим алгоритм Евклида:
- Делим 60 на 48 и получаем остаток 12.
- Затем делим 48 на 12 и получаем остаток 0.
- Так как остаток равен 0, то НОД чисел 48 и 60 равен последнему ненулевому остатку, т.е. 12.
Пример 3:
Для нахождения НОД чисел 35 и 42, применим алгоритм Евклида:
- Делим 42 на 35 и получаем остаток 7.
- Затем делим 35 на 7 и получаем остаток 0.
- Так как остаток равен 0, то НОД чисел 35 и 42 равен последнему ненулевому остатку, т.е. 7.
Аналогично можно использовать алгоритм Евклида для нахождения НОД больших чисел. Он основан на простых математических операциях и может быть легко реализован в программировании.
Основная идея алгоритма заключается в последовательном вычитании меньшего числа из большего до тех пор, пока эти числа не станут равными. Полученное число будет являться искомым НОД двух исходных чисел.
Алгоритм Евклида имеет следующие преимущества:
- Простота реализации. Алгоритм легко понять и реализовать на любом языке программирования.
- Высокая скорость работы. Алгоритм имеет линейную сложность, то есть его время выполнения пропорционально числу итераций, которое зависит от входных данных.
- Универсальность. Алгоритм может применяться для нахождения НОД как для целых чисел, так и для дробных чисел.
- Использование алгоритма Евклида в других алгоритмах. Алгоритм Евклида является основой для ряда других алгоритмов, таких как расширенный алгоритм Евклида для нахождения обратного элемента по модулю.
Целесообразность применения алгоритма Евклида для нахождения НОД обусловлена его эффективностью и простотой реализации. Он широко используется в различных областях, таких как криптография, математика, информатика и другие.



