Геометрия - это раздел математики, изучающий формы, размеры, относительное положение и свойства геометрических объектов. Практическое значение геометрии трудно переоценить, поскольку она позволяет нам анализировать и решать разнообразные пространственные задачи.
Однако, чтобы построить логическую систему геометрии, необходимо определить основные положения, которые не должны доказываться, а принимаются на веру. Такие основные положения называются аксиомами, и они являются основой аксиоматического метода геометрии.
Одной из основных аксиом геометрии в 7 классе является аксиома о равенстве отрезков. Она гласит, что если два отрезка равны между собой, то они имеют одинаковую длину. Данная аксиома позволяет нам сравнивать отрезки и устанавливать их равенство или неравенство.
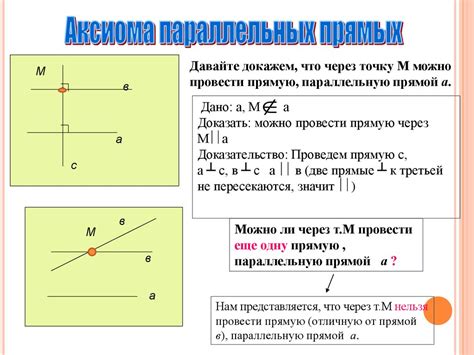
Другой важной аксиомой является аксиома о параллельных прямых. Она утверждает, что через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной. Эта аксиома определяет понятие "параллельной прямой" и является ключевой для изучения свойств параллельных и пересекающихся прямых.
Аксиома геометрии 7 класс
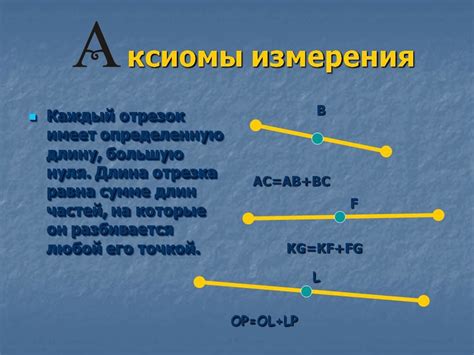
Одной из таких аксиом является аксиома о существовании отрезка. Эта аксиома утверждает, что между любыми двумя точками можно провести отрезок, который будет иметь конечную длину. Это предположение позволяет строить и изучать отрезки и их свойства, такие как равенство и сравнение.
Другой важной аксиомой является аксиома о равенстве отрезков. Она утверждает, что если два отрезка имеют одинаковую длину, то они равны друг другу. Это предположение позволяет сравнивать и классифицировать отрезки по их длине, что является основой для изучения геометрических фигур и их свойств.
Аксиома о прилежащих углах также играет важную роль в геометрии 7 класса. Согласно этой аксиоме, если два угла имеют общую вершину и стороны одного угла лежат на продолжении сторон другого, то эти углы являются смежными, или прилежащими. Это предположение позволяет изучать и классифицировать углы и их свойства в геометрии.
Таким образом, аксиомы геометрии 7 класса позволяют ученикам строить предположения и доказывать различные утверждения, основываясь на неразрешимых положениях. Они играют ключевую роль в формировании базовых навыков и понимании геометрических принципов и законов.
Определение аксиомы
Аксиомы геометрии формулируются так, чтобы быть логически связанными и простыми для понимания. Они принимаются как истины, которые не были и не могут быть доказаны с помощью других аксиом или теорем.
Понимание и усвоение аксиом геометрии необходимо для построения логической цепочки доказательств и развития геометрического мышления. Аксиомы геометрии 7 класс являются базовым материалом для дальнейшего изучения геометрии и построения более сложных доказательств в старших классах.
Ключевые положения аксиомы геометрии
Одно из ключевых положений аксиомы геометрии - это равенство сторон и углов. Оно основывается на сравнении объектов в геометрии. Если две стороны или два угла равны, то они могут быть заменены друг другом в равенстве, а результат будет сохраняться. Например, в треугольнике, если две стороны равны, то два угла прилежащие к этим сторонам также будут равны.
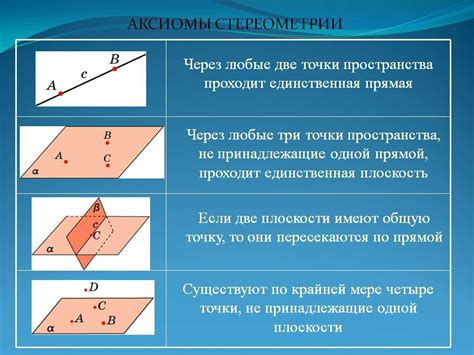
Второе ключевое положение аксиомы геометрии - это параллельность прямых. Оно утверждает, что если две прямые лежат в одной плоскости и не пересекаются, то они параллельны. Таким образом, параллельные прямые не имеют точек пересечения и продолжаются бесконечно в одном направлении.
Сущность аксиомы геометрии

Сущность аксиомы геометрии состоит в том, что она задает базовые правила и условия для проведения геометрических операций и построений. Она определяет, какие свойства и соотношения могут считаться верными в геометрическом пространстве.
Аксиомы геометрии не могут быть доказаны или выведены из других положений, так как они принимаются безусловно. Они являются первичными и не зависят от других геометрических утверждений или теорий.
Аксиомы геометрии могут иметь различные формулировки и варианты, но их сущность остается неизменной. Они служат фундаментом для развития геометрии и построения более сложных доказательств и теорем.
Важно понимать, что аксиомы геометрии - это не просто условия, которые признаются и принимаются в геометрии, они устанавливают основные правила и законы, которые лежат в основе всей геометрической системы.
Применение аксиомы геометрии в 7 классе
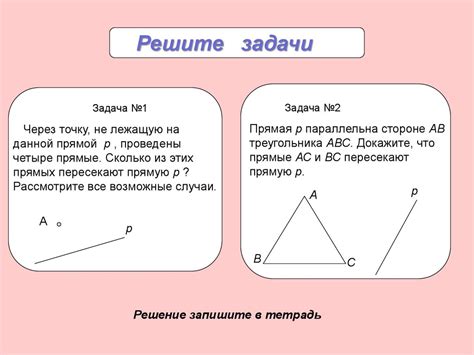
Применение аксиомы геометрии в 7 классе позволяет:
- Сравнивать и классифицировать геометрические фигуры;
- Находить свойства и характеристики фигур;
- Доказывать различные утверждения с использованием аксиом и ранее изученных понятий;
- Решать геометрические задачи, основываясь на аксиомах и знаниях о геометрических фигурах.
Одной из важнейших аксиом геометрии является аксиома о равенстве углов. Она гласит, что если два угла равны, то их соответствующие стороны равны. Эта аксиома позволяет ученикам решать задачи на нахождение неизвестных углов и строить фигуры с заданными углами.
Еще одной аксиомой геометрии в 7 классе является аксиома о равенстве треугольников. Согласно этой аксиоме, если три стороны одного треугольника равны соответственным сторонам другого треугольника, то эти треугольники равны. Эта аксиома позволяет ученикам доказывать и находить равенство треугольников в различных задачах.
Таким образом, применение аксиомы геометрии в 7 классе является основой для построения логической цепочки рассуждений, анализа геометрических объектов и решения геометрических задач. Оно помогает ученикам развивать умение работать с геометрическими фигурами и применять полученные знания на практике.



