На страницах школьных учебников математики нередко встречается выражение a + b в квадрате. Но что оно означает и как его рассчитать? В данной статье мы подробно рассмотрим эту формулу, чтобы вы могли легко разобраться в ее сути и применении.
Выражение a + b в квадрате можно прочитать как "а плюс б возводят в квадрат". Это означает, что оба слагаемых нужно возвести в квадрат, а затем сложить получившиеся результаты. Получается следующая формула: (a + b)².
Давайте рассмотрим пример, чтобы наглядно проиллюстрировать, как работает эта формула. Предположим, что a = 3 и b = 5. Тогда a + b = 3 + 5 = 8. Теперь возводим это число в квадрат: 8² = 64. Получается, что (3 + 5)² = 64.
Формула a + b в квадрате широко применяется в различных областях математики и физики. Она может использоваться, например, для решения уравнений, поиска корней, анализа данных и создания математических моделей. Понимать основы этой формулы можно и без глубоких знаний в математике, так как она часто используется в повседневной жизни.
Что такое А плюс b в квадрате?
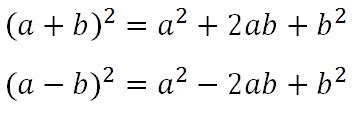
Формула А плюс b в квадрате имеет вид (А + b)² и представляет собой квадрат суммы двух чисел.
При раскрытии скобок получаем: (А + b)² = А² + 2Аb + b², где А² - квадрат первого числа, 2Аb - удвоенное произведение первого и второго чисел, b² - квадрат второго числа.
Формула может применяться в различных математических задачах, например, при решении квадратных уравнений, вычислении площади некоторых геометрических фигур, а также в физике и инженерии.
| Примеры расчетов по формуле: | Результат: |
|---|---|
| Если A = 3 и b = 4 | (3 + 4)² = 49 |
| Если A = 5 и b = 2 | (5 + 2)² = 49 |
| Если A = -2 и b = 3 | (-2 + 3)² = 1 |
Использование формулы позволяет упростить вычисления и получить более компактную запись результатов.
Формула расчета А плюс б в квадрате
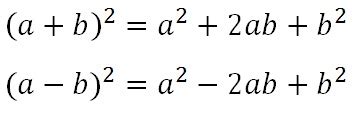
Формула расчета А плюс б в квадрате используется для вычисления квадрата суммы двух чисел. Формула записывается следующим образом: (А + б)^2. При использовании этой формулы необходимо сложить два числа и затем возвести полученную сумму в квадрат.
Пример расчета:
- Пусть А = 3 и б = 5.
- Сумма А и б равна 3 + 5 = 8.
- Возводим полученную сумму в квадрат: 8^2 = 64.
Таким образом, результатом формулы расчета А плюс б в квадрате, где А = 3 и б = 5, является число 64.
Формула расчета А плюс б в квадрате может использоваться в различных областях, например, в математике, физике, программировании и т.д. Ее результат может быть полезным при решении различных задач и вычислениях.
Как использовать формулу А плюс б в квадрате?
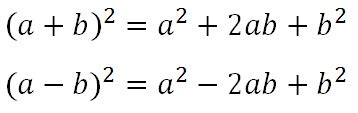
Формула А плюс б в квадрате представляет собой способ расчета квадрата суммы двух чисел. Данная формула особенно полезна в математике и физике для упрощения вычислений и анализа данных.
Чтобы использовать формулу А плюс б в квадрате, необходимо:
- Возьмите два числа, которые нужно сложить.
- Просуммируйте эти числа.
- Возведите полученную сумму в квадрат.
Итак, допустим у нас есть два числа: А и б. Для примера возьмем А = 3 и б = 2.
Сначала сложим эти числа: 3 + 2 = 5.
Затем возведем полученную сумму в квадрат, используя формулу: (3 + 2)² = 5² = 25.
Таким образом, результатом вычисления формулы А плюс б в квадрате для чисел 3 и 2 будет 25.
Усложнение вычислений возможно путем изменения значений чисел А и б.
Благодаря формуле А плюс б в квадрате можно более эффективно проводить вычисления, особенно при работе с большими данными или при использовании в сложных математических моделях.
Примечание: Важно помнить, что при использовании данной формулы необходимо правильно записывать и расставлять знаки операций и квадратов, чтобы избежать ошибок в результате.
Примеры расчета (А + б) в квадрате
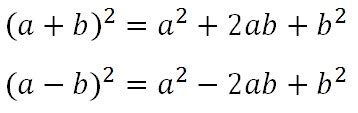
Давайте рассмотрим несколько примеров расчета формулы (А + б) в квадрате:
- Пример 1: Если значение А равно 2, а значение б равно 3, то (2 + 3)2 = 52 = 25.
- Пример 2: Предположим, что А равно -1, а б равно 4. Тогда (-1 + 4)2 = 32 = 9.
- Пример 3: Пусть А = 0 и б = 2. Тогда (0 + 2)2 = 22 = 4.
Это только несколько примеров, и вы можете использовать эту формулу для расчета более сложных значений А и б.
Значение и применение А плюс б в квадрате
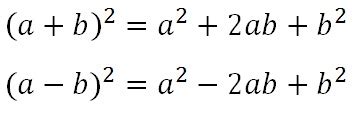
Формула А плюс б в квадрате представляет собой алгебраическое выражение, где значение переменной А складывается с квадратом значения переменной б. Такая формула активно используется в математике, физике и других научных дисциплинах.
Значение А плюс б в квадрате полезно во многих ситуациях, особенно при работе с уравнениями, анализе данных и моделировании. Общая формула для расчета значения выражения А плюс б в квадрате выглядит следующим образом:
(А + б)² = А² + 2Аб + б²
Использование этой формулы позволяет сократить и упростить вычисления в различных задачах. Например, при решении квадратных уравнений можно применить формулу А плюс б в квадрате для раскрытия скобок и дальнейшего анализа выражения.
Приведем пример: у нас есть квадратное уравнение x² + 4х + 4. Чтобы найти его решение, можно применить формулу А плюс б в квадрате:
(х + 2)² = х² + 2х * 2 + 2² = х² + 4х + 4
Таким образом, раскрытие скобок и применение формулы позволяет упростить уравнение и найти его корни. Знание формулы А плюс б в квадрате помогает в решении различных задач и облегчает математические вычисления в научных и практических областях.
Свойства формулы A плюс B в квадрате
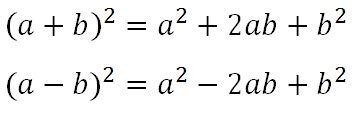
1. Раскрытие скобок:
Формула (A + B)² раскрывается по формуле квадрата суммы двух слагаемых:
(A + B)² = A² + 2AB + B²
2. Обратное раскрытие скобок:
Если известно значение квадрата суммы двух слагаемых (A + B)², то можно найти значения каждого слагаемого по формуле:
A² = (A + B)² - 2AB - B²
B² = (A + B)² - 2AB - A²
3. Сокращение формулы:
Иногда формула A² + 2AB + B² может быть сокращена до (A + B)², если некоторые слагаемые равны нулю или есть дополнительные ограничения на значения переменных A и B.
4. Практическое использование:
Формула A плюс B в квадрате широко применяется в математике, физике и других науках. Например, она может использоваться для нахождения площади квадрата, построенного на гипотенузе прямоугольного треугольника (теорема Пифагора), или для определения суммы и разности двух чисел в алгебре.
Таким образом, общая формула выглядит так: (a + b)² = a² + 2ab + b².
Расчет квадрата суммы двух чисел может быть полезен в различных областях, таких как физика, математика, экономика и др. Он позволяет быстро находить значение, например, в задачах с градусами или квадратными корнями.
Приведем несколько примеров использования формулы:
- Расчет площади квадрата, если известны длины его сторон.
- Нахождение суммы квадратов двух чисел.
- Определение значения переменной в уравнении, если известны значения остальных переменных.
- Вычисление полной мощности электрической цепи.
Использование формулы для нахождения квадрата суммы двух чисел упрощает вычисления и повышает эффективность решения задач, связанных с квадратами и расчетами на основе них. Кроме того, это также помогает развивать логическое мышление и математические навыки.



