Определение отличий между кратной и дольной величиной является важной задачей в науке и повседневной жизни. Кратные и дольные величины представляют собой две разные концепции, которые используются для измерения и описания различных физических и математических явлений.
Кратные величины представляют собой меру, которая делится на равные части, например, метры, граммы и секунды. Они используются для измерения длины, массы и времени соответственно. С другой стороны, дольные величины представляют собой одну часть из целого, например, доли и проценты. Они используются для измерения частей от общего количества или отношения между величинами.
Существует несколько способов определить отличия между кратными и дольными величинами. Первый способ - это рассмотрение самой величины и ее значения. Если величина имеет дробное значение или указание на часть от целого, то она является дольной. Если величина имеет целочисленное значение и не указывает на часть или долю целого, то она является кратной.
Что такое кратная и дольная величина?
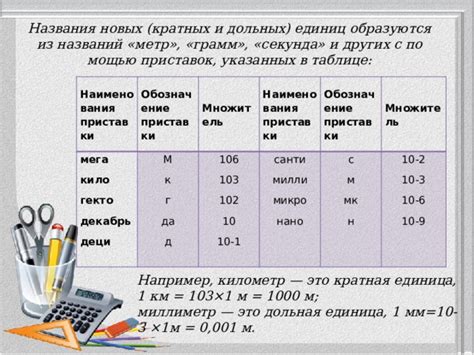
Кратная величина представляет собой числовое значение, которое является результатом умножения другой величины на целое число. Например, если у нас есть величина "длина" и мы знаем ее значение в метрах, то кратной величиной может быть "длина" в дециметрах (1 метр = 10 дециметров), "длина" в километрах (1 метр = 0.001 километра) и т.д. Кратные величины позволяют нам измерять и описывать различные аспекты одной и той же величины.
С другой стороны, дольная величина представляет собой долю или часть от общего значения величины. Например, если у нас есть величина "длительность времени" и ее значение составляет 10 часов, то дольной величиной может быть "длительность времени" в минутах (1 час = 60 минут), "длительность времени" в секундах (1 час = 3600 секунд) и т.д. Дольные величины позволяют нам разбить общее значение на более мелкие единицы и проводить более детальные измерения.
Использование кратных и дольных величин играет важную роль в научных и технических расчетах, а также в повседневной жизни. Знание различий между ними позволяет проводить точные измерения и оперировать числовыми значениями в более удобной и понятной форме.
Понятия кратной и дольной величины

Кратная величина – это число, кратное другому числу. Более конкретно, если одно число является кратным другому, то можно умножить первое число на некоторое целое число, чтобы получить второе число. Например, число 12 кратно числу 3, потому что 12 можно получить путем умножения числа 3 на 4 (3 * 4 = 12).
Дольная величина – это обратное отношение к кратной величине. Если одно число является дольной величиной другого числа, то эту долю можно получить путем деления первого числа на второе. Например, число 2 является долей числа 8, потому что 8 можно поделить на 4 для получения 2 (8 / 4 = 2).
Важно отметить, что кратная и дольная величины могут быть представлены разными единицами измерения. Например, кратная величина может описывать увеличение или уменьшение экспоненциальных значений, таких как мега или микро, в то время как дольная величина может описывать отношение двух чисел в единицах массы или времени.
Разница между кратной и дольной величиной
Кратные величины обозначаются как целые числа или их множества, в то время как дольные величины представлены десятичными дробями или рациональными числами.
Если мы рассмотрим пример, где имеется величина, которую можно поделить на другую величину без остатка, то это будет кратная величина. Например, если у нас есть 12 яблок, и мы решим поделить их на 3 группы по 4 яблока, то каждая группа будет содержать кратные величины. В данном случае, кратная величина будет 4 яблока, поскольку она является делителем исходной величины.
В отличие от этого, дольная величина будет представлена в виде десятичной дроби или рационального числа. Например, если мы рассмотрим пример скорости движения автомобиля, и он проезжает 100 километров за 2 часа, то соответствующая мера скорости будет дольной величиной в виде 50 км/час.
Таким образом, кратные и дольные величины имеют свои уникальные свойства и представления, которые позволяют нам более точно измерять и описывать физические явления в нашей среде.
Как определить, является ли величина кратной или дольной?

1. Использование деления с остатком
Если величина делится без остатка на другую величину, то она является кратной. Например, если число 12 делится на 3 без остатка, значит оно кратно 3. Для определения, является ли величина дольной, нужно проверить, делится ли она на другую величину с остатком. Например, число 7 не делится на 3 без остатка, значит оно является дольным относительно числа 3.
2. Отношение величин
Еще один способ определить, является ли величина кратной или дольной, – это сравнить отношение этих величин. Если одна величина является результатом умножения другой на целое число, то первая величина будет кратной, а вторая – дольной. Например, если отношение 12 к 3 равно 4, то 12 является кратной величиной относительно 3.
3. Порядок возрастания/убывания величин
Третий способ определить, является ли величина кратной или дольной, основан на порядке возрастания или убывания величин. Если величина увеличивается в результате умножения на целое число, то она является кратной. Если же она уменьшается, то она является дольной. Например, если последовательность величин 2, 4, 6, 8, 10, то можно сказать, что все числа кратные 2. Если же последовательность величин 10, 8, 6, 4, 2, то можно сказать, что все числа дольные относительно 10.
Способ №1: Исследование делителей
Первый способ определения отличий между кратной и дольной величиной основан на анализе делителей этих величин. Чтобы понять, кратная ли величина или нет, нужно проверить, делится ли она равномерно на другую величину без остатка.
Для начала выберем две величины, которые мы собираемся сравнить. Допустим, у нас есть число 12 и число 3. Чтобы узнать, является ли 12 кратным числом 3, мы исследуем делители числа 12.
Делителями числа 12 являются числа, на которые 12 делится без остатка. В данном случае, делителями числа 12 являются 1, 2, 3, 4, 6 и 12.
Теперь нам нужно проверить, входит ли число 3 в этот список делителей. Если число 3 присутствует, то 12 является кратным числом 3. Если же число 3 отсутствует в списке делителей, то 12 не является кратным числом 3.
В данном случае, число 3 присутствует в списке делителей числа 12. Это означает, что 12 является кратным числом 3.
Использование данного способа позволяет определить, является ли одна величина кратной другой без необходимости выполнения длительных вычислений.
Способ №2: Использование десятичной записи
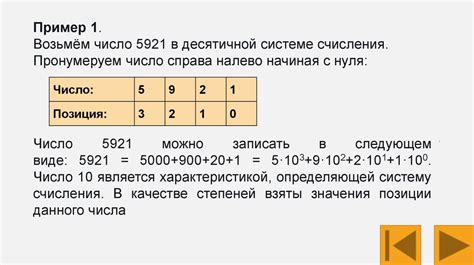
Например, пусть у нас есть число 0.5. Это является кратной величиной, потому что оно имеет только один десятичный знак после запятой - 5. Если бы мы имели число 0.333..., то это было бы дольной величиной, потому что оно имеет бесконечное число десятичных знаков 3.
Другой пример: число 0.25. Это кратная величина, потому что оно имеет два десятичных знака после запятой - 2 и 5. В то же время, число 0.333... будет дольной величиной, так как у него бесконечное число десятичных знаков 3.
Использование десятичной записи позволяет определить, является ли число кратной или дольной величиной с использованием визуального анализа его десятичной части.
Однако нужно помнить, что некоторые дроби могут быть представлены как кратные или дольные величины в зависимости от точности их записи. Например, число 1/3 может быть записано как 0.333... или как 0.34, в зависимости от выбранной точности.
Способ №3: Примеры кратных и дольных величин
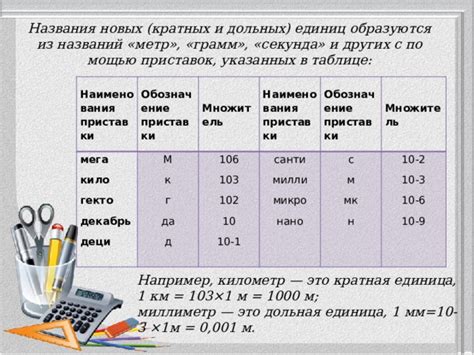
Чтобы лучше понять различия между кратной и дольной величиной, рассмотрим несколько примеров.
Пример кратной величины:
Представим ситуацию, где у нас есть 12 яблок и мы хотим поделить их на равные группы по 3 яблока в каждой. В данном случае количество яблок (12) является кратной величиной, а количество яблок в каждой группе (3) является дольной величиной. Мы можем получить 4 группы по 3 яблока в каждой. Таким образом, 12 яблок являются кратной величиной по отношению к группам по 3 яблока.
Пример дольной величины:
Рассмотрим ситуацию, когда у нас есть 5 книг и мы хотим поделить их между 2 людьми. В данном случае количество книг (5) является дольной величиной, так как мы не можем поделить их равномерно между двумя людьми. Один из людей получит 2 книги, а другой - 3 книги. В этом случае количество книг не делится равномерно на группы, поэтому оно является дольной величиной.
Таким образом, примеры кратной и дольной величин помогают наглядно продемонстрировать различия между ними. Кратная величина делится на равные группы или части, в то время как дольная величина не может быть разделена равномерно.



